Friedman-Test

Friedman-Test

  • 21. März 2017
  • Posted by: Mika
Keine Kommentare

Liegen Dir drei oder mehr abhängige Stichproben einer mindestens ordinalskalierten Zufallsvariablen X vor, so kannst Du mit dem Friedman-Test prüfen, ob zwischen den Stichproben Unterschiede bezüglich der Lageparameter bestehen. Weil er keine Verteilungsvoraussetzung benötigt und auch auf kleine Stichproben angewendet werden kann, stellt er eine Alternative zur Varianzanalyse (ANOVA) dar, wenn deren Voraussetzungen nicht erfüllt sind.

Aufstellen von Hypothesen

H_0: Es bestehen keine signifikanten Unterschiede zwischen den Lageparametern der Stichproben.

H_1: Es bestehen signifikanten Unterschiede zwischen den Lageparametern der Stichproben.

Stell Dir vor, Dein Unternehmen beauftragt eine Gesundheitsberatung, ein Programm zur Gewichtsreduktion der Mitarbeiter durchzuführen. Dabei wird an k=3 Terminen das Gewicht von n=12 Mitarbeitern anonym dokumentiert. Du erhältst die ersten vier Spalten der nachfolgenden Tabelle und sollst prüfen, ob die Durchführung des Programms signifikante Änderungen des Gewichts der Mitarbeiter bewirkt hat:

lfd. Nr. Gewicht … innerhalb der Messungen der Person i:
Rang ihres Gewichtes …
i … zu Beginn … in der Mitte … am Ende … am Anfang R_{i1} … in der Mitte R_{i2} … am Ende R_{i3}
1 92,3 kg 88,4 kg 87,2 kg 3 2 1
2 108,0 kg 103,5 kg 104,5 kg 3 1 2
3 90,9 kg 90,2 kg 88,7 kg 3 2 1
4 76,4 kg 73,4 kg 72,6 kg 3 2 1
5 95,9 kg 89,6 kg 89,2 kg 3 2 1
6 107,9 kg 98,2 kg 95,0 kg 3 2 1
7 73,2 kg 67,7 kg 64,9 kg 3 2 1
8 77,2 kg 73,1 kg 73,0 kg 3 2 1
9 98,2 kg 92,4 kg 93,7 kg 3 1 2
10 93,9 kg 91,6 kg 92,4 kg 3 1 2
11 113,5 kg 110,5 kg 108,3 kg 3 2 1
12 92,2 kg 90,7 kg 89,9 kg 3 2 1
Rangsummen 36 21 15

Wie wird der Friedman-Test durchgeführt?

Für die Messungen jeder Person i trägst du in den letzten drei Spalten die Rangfolge R_{ij} ihrer persönlichen Gewichtsmessungen ein. Person 1 beispielsweise hat das niedrigste Gewicht am Ende (R_{13}=1), das höchste bei der ersten Messung (R_{11}=3); Person 9 weist ebenfalls das höchste Gewicht zu Beginn auf (R_{91}=3),das niedrigste in der Mitte(R_{92}=1) und am Ende einen mittleren Wert (R_{93}=2).

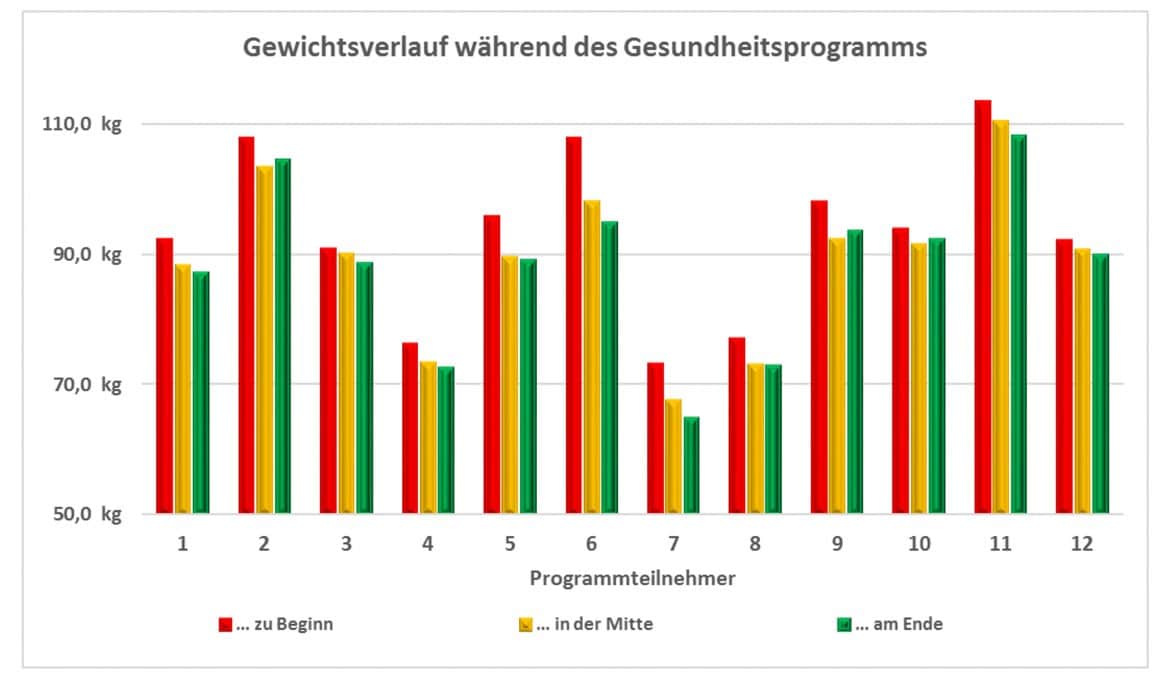
Friedmann-Test

Aus diesen individuellen Rangwerten bildest Du dann in der letzten Zeile die Rangsummen pro Messung. Falls keine signifikanten Unterschiede zwischen den Stichproben bestehen, wären auftretende Gewichtsveränderungen zufällig, und es müsste jeder Rang zu jedem Messzeitpunkt etwa gleich häufig vorkommen. Die Rangsummen pro Termin sollten dann etwa gleich hoch sein. Je stärker sie differieren, umso größer ist die Wahrscheinlichkeit, dass die Lageparameter der drei Stichproben tatsächlich Unterschiede aufweisen.

Die Teststatistik

Friedman betrachtet zum einen das n-fache der Summe der quadratischen Abweichungen zwischen den Stichprobenmitteln und dem Gesamtmittel der Ränge, zum anderen die Gesamtvarianz aller Rangplätze. Seine Teststatistik, die sich in den Ausdruck auf der rechten Seite vereinfachen lässt, falls keine Ranggleichheit vorkommt, bildet den Quotienten aus beiden:

    \begin{equation*} \chi^2 = \frac {n \cdot \displaystyle \sum_{j=1}^k (\bar R_{\cdot j} - \bar R)^2} {\frac 1 {n \cdot (k-1)} \cdot \displaystyle \sum_{i=1}^n \sum_{j=1}^k ( R_{ij} - \bar R)^2 } =\frac {12} {n \cdot k \cdot (k+1)} \cdot \sum_{i=1}^k \cdot \left( \sum_{j=1}^n R_{ij}\right)^2 - 3 \cdot n\cdot (k+1) \end{equation*}

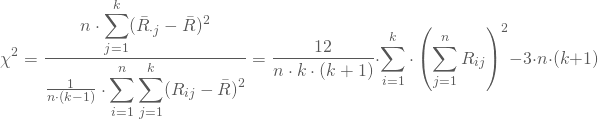
Für n > 15 oder k > 4 ist die Prüfgröße asymptotisch \chi^2-verteilt mit (k-1) Freiheitsgraden; für kleinere Stichproben musst Du die spezielle Tabelle des Friedman-Test verwenden. Hier ergibt diese Tabelle zum Niveau von 5\% für n=12 und k=3 einen kritischen Wert von 6,17.

Dein Testergebnis lautet:

    \begin{equation*} \chi^2 = \frac {12} {12 \cdot 3 \cdot 4} \cdot (36^2 + 21^2 + 15^2 ) - 3 \cdot 12\cdot 4 = 19,5 > 6,71 = \chi^2_{kr} \end{equation*}

Mit einer Irrtumswahrscheinlichkeit von 5\% schließt Du, dass das durchgeführte Gesundheitsprogramm wirksam war.