Teststatistik

Teststatistik

  • 18. November 2016
  • Posted by: Mika
Keine Kommentare

Die Teststatistik ist eine Stichprobenfunktion, die Du innerhalb von Hypothesentests für die Entscheidung über Verwerfen oder Nicht-Verwerfen einer Hypothese verwendest. Alternative Bezeichnungen für sie sind Prüfgröße oder Testgröße.

Zunächst gehst Du davon aus, dass Deine Stichprobenergebnisse Realisationen von Zufallsvariablen sind, die sich aus den Parametern der Grundgesamtheit und Zufallseinflüssen zusammensetzen.

Aufgrund der für die Grundgesamtheit angenommenen Parameter und/oder der Verteilung konstruierst Du eine Stichprobenfunktion. Diese folgt je nach Voraussetzungen und in Abhängigkeit der Informationen, die Du über sie hast, einer statistischen Verteilungsfunktion. Für diese kannst Du angeben, mit welcher Wahrscheinlichkeit jeder theoretische mögliche Wert der Stichprobenfunktion unterschritten wird.

Beispielrechnung

Stell Dir vor, Du bist auf der Suche nach einer neuen günstigen Wohnung in Frankfurt und sprichst mit einem Makler. Dieser behauptet, der aktuelle Durchschnittswert der Quadratmeterpreise liege bei 15 €. Das scheint Dir sehr hoch angesetzt. Daher erhebst Du eine Stichprobe aus 10 aktuellen Wohnungsangeboten, die einen durchschnittlichen Quadratmeterpreis von 13,70 € ergibt.

Als nächstes möchtest Du mit einer Irrtumswahrscheinlichkeit von α = 5% testen, ob die Aussage des Maklers durch Deine Erhebung wiederlegt wird, und stellst dazu folgende Hypothesen auf.

    \begin{equation*} H_0:\mu\geq 15 \quad \text{gegen}\quad H_1<15 \end{equation*}

Falls die Realisation der Stichprobe kleiner als Dein kritischer Wert ist, wird die Nullhypothese verworfen, anderenfalls nicht. Dabei soll die Wahrscheinlichkeit, dass Du die Nullhypothese irrtümlich verwirfst, 5% betragen. Den kritischen Wert erhältst Du folglich als den Wert, den die jeweilige Verteilungsfunktion mit einer Wahrscheinlichkeit von 5% nicht übersteigt.

Konstruktion der Teststatistik

Die Konstruktion Deiner Teststatistik hängt nun davon ab, welche Voraussetzungen gegeben sind:

  1. Von den Mietpreisen pro Quadratmeter in Frankfurt weißt Du, dass sie normalverteilt sind und eine Varianz von 4 aufweisen. Dann ist der Durchschnitt Deiner Stichprobe ebenfalls eine normalverteilte Zufallsvariable 

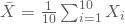 \bar X=\frac 1{10}\sum_{i=1}^{10}X_i mit dem gleichen Mittelwert 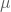\mu und der Varianz 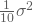\frac{1}{10}\sigma^2. Setzt Du dann die Werte der Stichprobe ein, standardisierst sie mit dem behaupteten Mittelwert 15 und der Standardabweichung 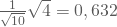\frac{1}{\sqrt{10}}\sqrt 4=0,632, so erhältst Du als Teststatistik einen standardnormalverteilten Prüfwert, den Du mit dem kritischen Wert der Standardnormalverteilung 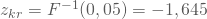z_{kr}=F^{-1}(0,05)=-1,645 vergleichst:Mit 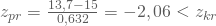z_{pr}=\frac{13,7-15}{0,632}=-2,06<z_{kr} wird die Nullhypothese verworfen.
  2. Kennst Du dagegen die Varianz der Grundgesamtheit nicht, musst Du sie aus Deiner Stichprobe schätzen als 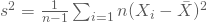s^2=\frac{1}{n-1}\sum_{i=1}n (X_i-\bar X)^2. In unserem Beispiel sei 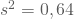s^2=0,64 berechnet. Dann folgt Deine Teststatistik, die standardisierte Zufallsvariable „durchschnittlicher Mietpreis“, einer t-Verteilung 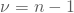\nu=n-1 Freiheitsgraden:Du musst also den Wert Deiner Testgröße mit dem kritischen 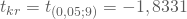t_{kr}=t_{(0,05;9)}=-1,8331 vergleichen.
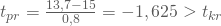    t_{pr}=\frac{13,7-15}{0,8}=-1,625>t_{kr} kann die Nullhypothese jetzt nicht verworfen werden.

Im Beispiel wird deutlich, dass die Testentscheidung umso vorsichtiger getroffen wird, je weniger Informationen vorhanden sind. Bei sonst gleicher Ausgangslage führt die Unkenntnis der Varianz in der Grundgesamtheit dazu, dass die Teststatistik einer t-Verteilung folgt und hier die Nullhypothese nicht mehr verworfen werden kann.

Interpretation am Beispiel der t-Verteilung

Die t-Verteilung verläuft im Zentrum flacher und ist endlastiger, das heißt, die Wahrscheinlichkeit für größere Abweichungen vom Mittelwert steigt, je kleiner die Stichprobe ist.

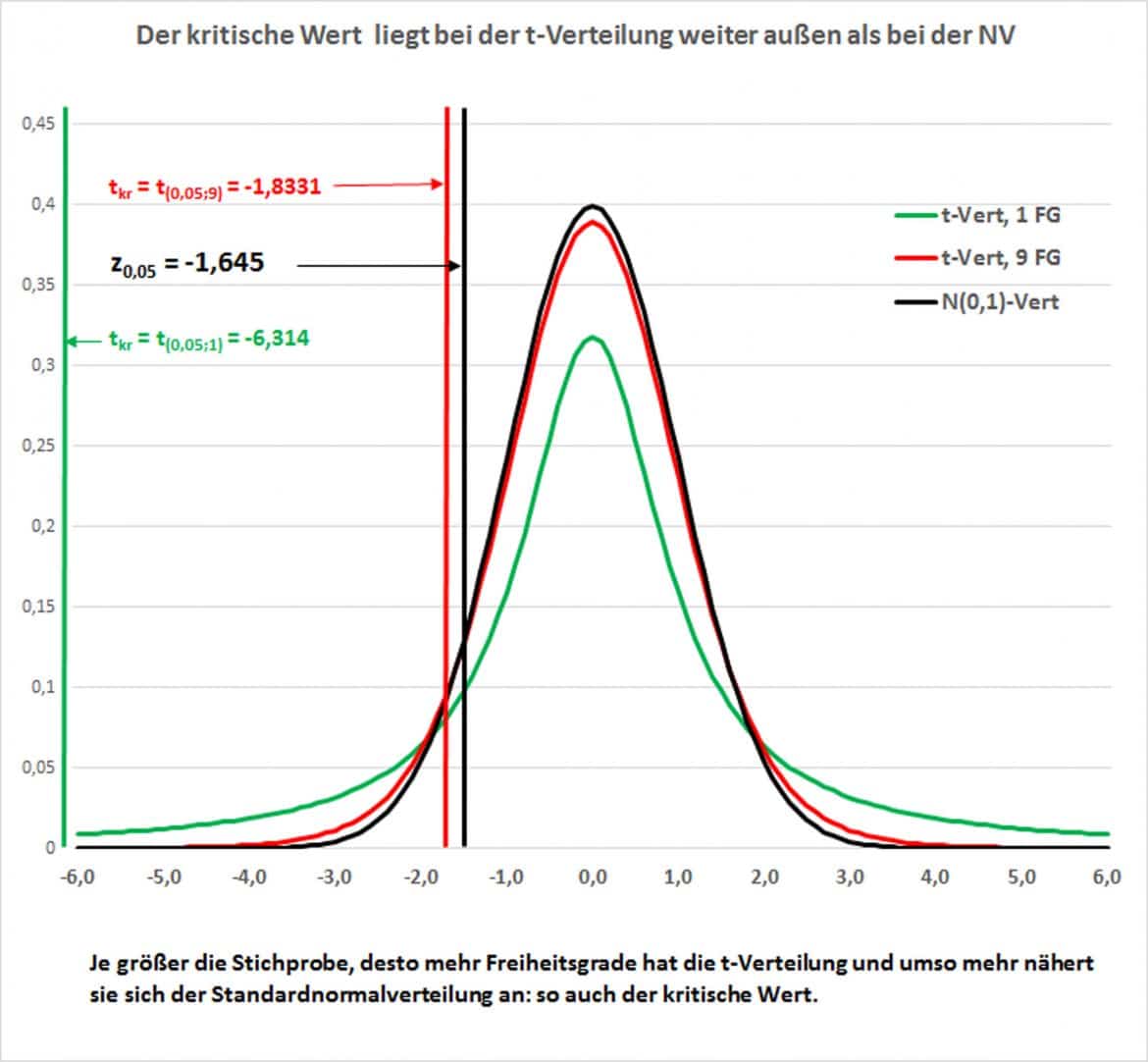
t-verteilung

Die Grafik zeigt, wie sich mit steigendem Umfang der Stichprobe die t-Verteilung an die Standardnormalverteilung anpasst und wie der kritische Bereich von extremer Position an den der Standardnormalverteilung rückt.

Je größer Du den Umfang n der Stichprobe wählst, desto kleiner wird die Varianz der Stichprobe durch den Faktor und desto weiter nähert sich die Funktion des standardisierten Stichprobenmittelwerts einer Standardnormalverteilung an. Dies ist gemäß des zentralen Grenzwertsatzes für n>100 gegeben.

\frac{1}{n-1}

Nach diesen Überlegungen erhebst Du eine Stichprobe vom Umfang n=120, die als Mittelwert = 14 und als s2 = )2 = 0,87 ergibt. Das überzeugt Dich und den Makler davon, dass der mittlere Quadratmeterpreis bei μ = 14 € liegt.

\bar x s^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar x)^2=0,87 \mu=14

Jetzt möchtest Du testen, ob die Varianz der Quadratmeterpreise in der Grundgesamtheit kleiner als 1 ist und suchst nach einer geeigneten Testgröße für den Test:

H0: σ2 > 1 gegen H1: σ2 ≤ 1

    \begin{equation*} H_0:\sigma^2>1\quad\text{gegen}\quad H_1:\sigma^2\leq 1 \end{equation*}

Die Summe von standardnormalverteilten und quadrierten Zufallsvariablen folgt einer 2-Verteilung mit (n-1) Freiheitsgraden.

\chi^2

Daher ist der Quotient : -verteilt. Du kannst die Teststatistik mit dem zugehörigen kritischen Wert  = 94,8 vergleichen:

\frac{(n-1)S_x^2}{\sigma^2}:\chi_{n-1}^2 \chi_{(119;\alpha)=94,8}
Mit = 103,53 > 94,8 wird die Nullhypothese, die Varianz der Grundgesamtheit sei größer als 1, mit einer Irrtumswahrscheinlichkeit von 5% verworfen.

\frac{119\cdot 0,87}{1}=103,53>94,8