Poweranalyse: Betafehler (Fehler 2. Art), Effekt, Teststärke, Optimaler Stichprobenumfang

Beim Durchführen von Hypothesentests stellst Du eine Nullhypothese auf und testest sie zu einem bestimmten Signifikanzniveau α, meist 5%. Die Wahrscheinlichkeit, Deine Nullhypothese zu verwerfen, obwohl sie gilt, ist damit auf maximal 5% gesetzt.

Nun gibt es über den Alphafehler hinaus weitere Einflussgrößen, die die „Qualität“ Deines Tests bestimmen:

• Fehler 2. Art oder Betafehler
• Größe des Effekts
• Umfang der Stichprobe

Du untersuchst das Lungenvolumen von Schülern. Du weißt, dass ihr durchschnittliches Lungenvolumen μ bei der Größe 170 cm bei vier Litern liegt und eine bekannte Varianz aufweist. Um zu testen, ob Leistungssport das Lungenvolumen auf 4,5 Liter erhöht, hast Du zunächst eine Stichprobe vom Umfang 120 erhoben. Dann hast Du einen Mittelwert von 4,4 Litern bestimmt. Damit kannst Du für den Mittelwert über den Zentralen Grenzwertsatz Normalverteilung annehmen.

Deine Hypothesen lauten:

   

Die Verteilung für den Mittelwert ist in der Grafik braun und der kritische Bereich, in dem Du einen Fehler 1. Art begehst, ist rot unterlegt eingezeichnet. Die blaue Linie zeigt den kritischen Wert Deines Tests.

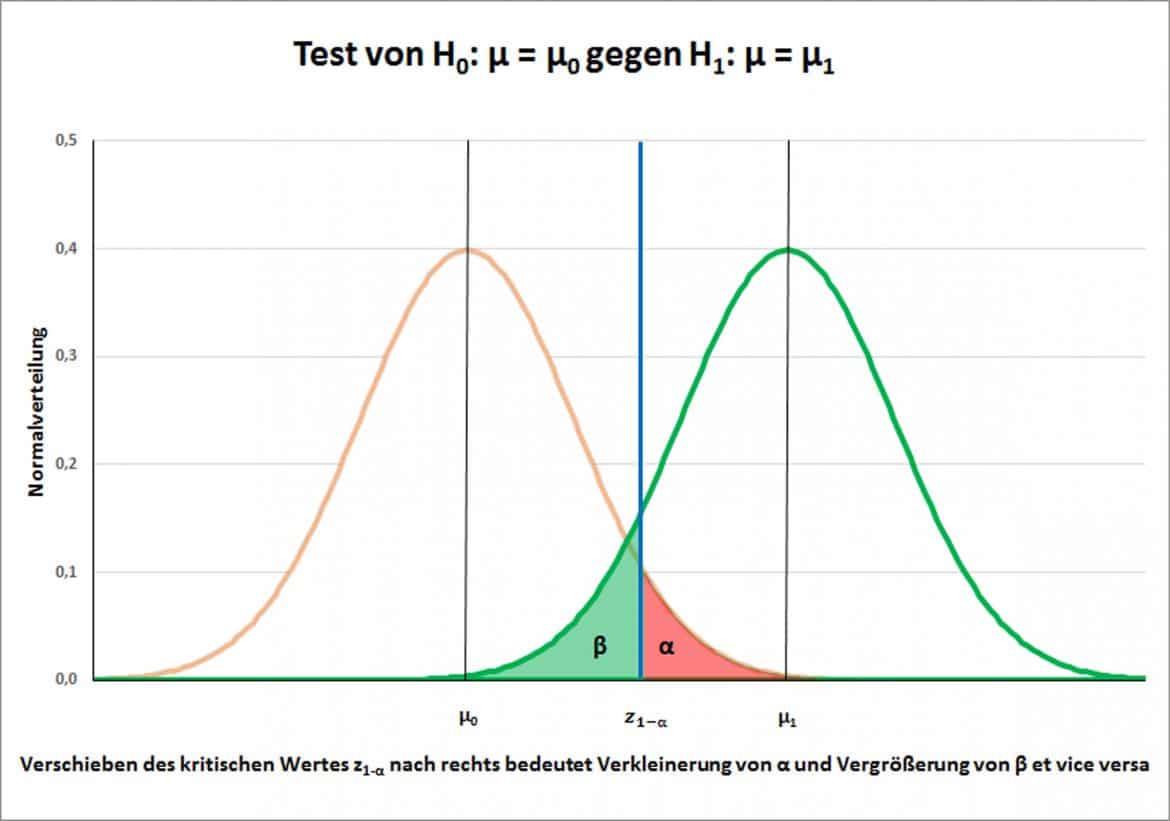
Die Testentscheidung mithilfe Deiner Prüfgröße kannst Du an der Grafik vollziehen: Ist , wird die Nullhypothese nicht verworfen, gilt , wird sie verworfen.

Die grüne Kurve ist die Verteilung unter . Falls gilt, liegt der erhöhte Mittelwert bei , und die Realisationen des Stichprobenmittelwerts streuen um . Auch hier sind an den Enden der Verteilung extreme Werte möglich. Die Grafik zeigt in Form des Betafehlers eine weitere Fehlermöglichkeit auf: Das unter de facto vergrößerte Lungenvolumen nicht als solches zu erkennen.

Der Betafehler

Mit Deinem für bestimmten kritischen Wert bestimmt sich die Größe des Betafehlers als Fläche unter der grünen Verteilungsfunktion links von . Der kritische Wert und damit die Trennung zwischen dem kritischen Bereich und dem Annahmebereich wird in der Grafik durch die blaue Linie dargestellt.

Du kannst in der Grafik erkennen, dass eine Verkleinerung des Alphafehlers eine Verschiebung des kritischen Wertes, nach rechts bewirkt. Dadurch wird direkt der Betafehler vergrößert. Umgekehrt bewirkt eine Vergrößerung des Alphafehlers eine Verschiebung des kritischen Wertes nach links und der Betafehler wird reduziert.

Die Power eines statistischen Tests

Unter der Power oder Mächtigkeit eines Tests versteht man die Wahrscheinlichkeit, eine de facto falsche Nullhypothese auch tatsächlich zu verwerfen, also keinen Betafehler zu machen. Im Beispiel heißt das, das tatsächlich erhöhte Lungenvolumen im Test auch festzustellen. Natürlich ist ein Test zum Niveau α umso mächtiger und umso besser, je kleiner der zugehörige -Fehler ist.

Während Du den Alphafehler eines Tests beliebig festlegen kannst, lässt sich der Betafehler nicht direkt kontrollieren. Aber er hängt neben der Größe von α unmittelbar von dem zu überprüfenden Effekt und von der Größe der Stichprobe ab.

Der Effekt

Unter dem Effekt versteht man die Differenz zwischen den beiden möglichen Mittelwerten. Je größer der zu testende Effekt ist, desto leichter sind die Hypothesen voneinander zu unterscheiden. Desto weiter entfernt voneinander liegen die Scheitelpunkte der Verteilungen und desto geringere Überlappungsbereiche gibt es. Grafisch verschiebt sich mit einer Vergrößerung des Effekts die grüne Funktion nach rechts. Weil der kritische Wert an seiner Stelle verbleibt, wird die Fläche unter der grünen Funktion links vom kritischen Wert damit kleiner.

Einfluss des Stichprobenumfangs

Die absolute Effektgröße Deines Tests ist normalerweise inhaltlich vorgegeben und methodisch nicht variabel. Da Du die Testentscheidung aber mithilfe von standardisierten Werten durchführst, lässt sich der standardisierte Effekt durch den Stichprobenumfang variieren. Je größer Du Deine Stichprobe wählst, umso geringer ist die Varianz des Mittelwertes, umso größer ist der standardisierte Effekt und umso weiter nach rechts verschiebt sich die grüne Funktion:

Für obigen Fall hast Du den Effekt mit gegeben, sowie die Varianz mit .

Die Tabelle zeigt den Einfluss des Stichprobenumfangs auf den standardisierten Effekt:

Stichprobenumfang	Varianz des Mittelwertes:	standardisierter Effekt:
n = 120	0,183	2,732
n = 500	0,089	5,618
n = 1000	0,063	7,937

In der zweiten Grafik siehst Du, wie die Power eines Test mit zunehmendem n steigt, weil sich die Kurve unter nach rechts verschiebt: für n=120 ist der Betafehler als Fläche unter der gelben Kurve bis zum Schnittpunkt mit relativ groß; für n=1000 als Fläche unter der blauen Kurve bis zum Schnittpunkt mit deutlich kleiner und für n=5000 vernachlässigbar gering.

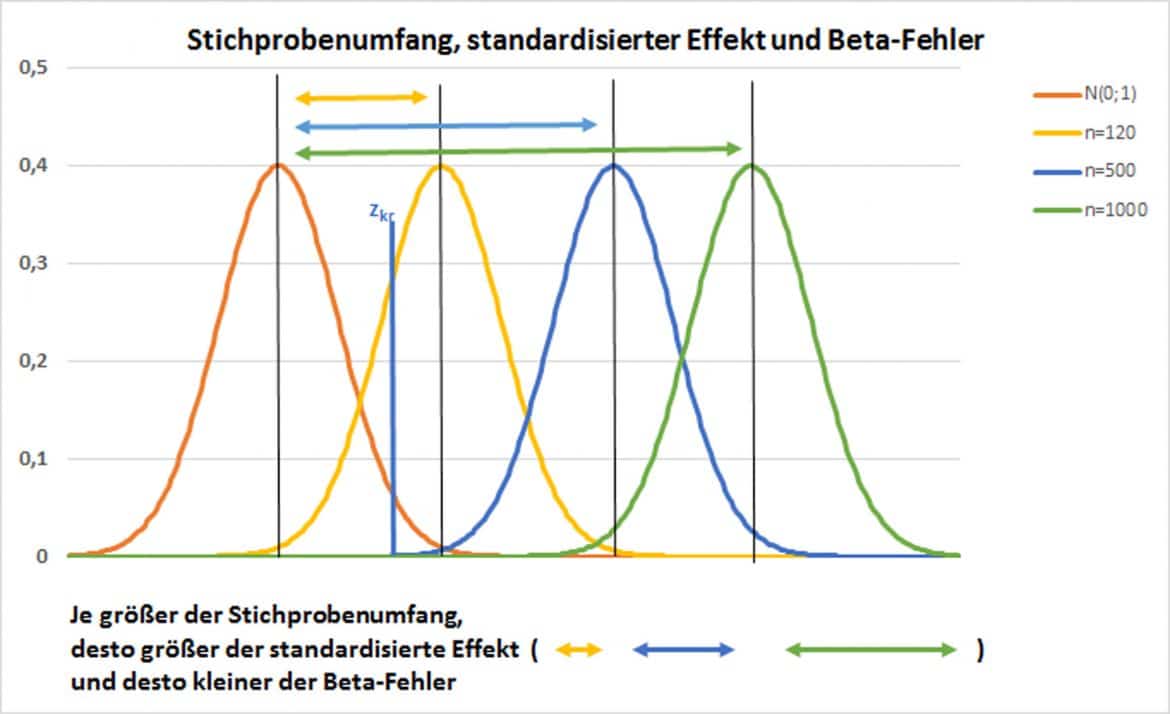
Für ein vorgegebenes Alpha und einen gegebenen Effekt kannst Du also durch die Wahl des Stichprobenumfangs den Betafehler so beeinflussen, dass er ein gewünschtes Fehlerniveau nicht überschreitet. Allgemein gilt dabei: Je größer der Effekt ist, den Du testen möchtest, desto leichter ist er zu erkennen und desto kleiner kannst Du den Stichprobenumfang wählen.

Anders herum formuliert: je größer die Stichprobe, desto geringer die Varianz des Stichprobenmittelwerts und desto größer ist der standardisierte Effekt. Eine Erhöhung der Stichprobe ist aber immer auch mit zusätzlichem Aufwand und vermehrten Kosten verbunden.

Poweranalyse

Die Poweranalyse untersucht das Zusammenspiel von Alpha- und Betafehler, Effekt und Stichprobengröße. Üblich ist es, den Betafehler viermal so groß wie den Alphafehler zu wählen, so dass beispielsweise bei ein von 20% angestrebt wird.

Bevor Du Deine Stichprobe erhebst, solltet Du möglichst die erforderliche bzw. optimale Stichprobengröße ermitteln. Zu diesen Überlegungen gibt es leistungsfähige Programmtools, mit denen Du die Poweranalyse durchführen kannst. Ein kostenloses Tool ist beispielsweise GPower.