Nullhypothese, Alternativhypothese (Gegenhypothese), Gerichtete Hypothese, Ungerichtete Hypothese

Nullhypothese, Alternativhypothese (Gegenhypothese), Gerichtete Hypothese, Ungerichtete Hypothese

  • 18. November 2016
  • Posted by: Mika
Keine Kommentare

Im ersten Schritt beim Durchführen eines Hypothesentests triffst Du eine geeignete Auswahl von Null- und Alternativhypothesen. Dabei überlegst Du, ob Du einen einseitigen oder zweiseitigen Test durchführen solltest. Im Falle eines einseitigen Tests überlegst Du zudem, in welche Richtung Du testen solltest.

Zweiseitiger Hypothesentest

Ein zweiseitiger oder ungerichteter Test überprüft die (ungerichtete) Nullhypothese, ob der Mittelwert der Stichprobe mit einem angenommenen Mittelwert \mu_0 der Grundgesamtheit übereinstimmt. Dagegen steht die Alternativhypothese, dass keine Übereinstimmung vorliegt:

    \begin{equation*} H_0:\mu=\mu_0 \quad \text{gegen} \quad H_1:\mu\neq\mu_0 \end{equation*}

Diesen Test wendest Du an, wenn Abweichungen des Mittelwertes in beide Richtungen bedeutsam sind.

Angenommen, ein Pharmaunternehmen stellt sein Medikament „SchmerzAde“ mit angegebenen 10 mg Wirkstoff her. Deine Aufgabe ist es, diese Angabe anhand einer Stichprobe zu überprüfen. Da sowohl eine größere als auch eine kleinere Wirkstoffmenge als angegeben zu vermeiden ist, entscheidest Du Dich für einen ungerichteten oder zweiseitigen Test.

Einseitiger Hypothesentest

Ein einseitiger oder gerichteter Test untersucht die (gerichtete) Nullhypothese, der Mittelwert Deiner Grundgesamtheit sei kleiner oder größer als ein zu betrachtender Wert, gegen die umgekehrt gerichtete Alternativhypothese:

    \begin{equation*} H_0:\mu=\mu_0 \quad \text{gegen} \quad H_1:\mu\geq\mu_0 \end{equation*}

oder

    \begin{equation*} H_0:\mu>\mu_0 \quad \text{gegen} \quad H_1:\mu\leq\mu_0 \end{equation*}

Den gerichteten Test wendest Du an, wenn Dich Abweichungen nur in eine Richtung interessieren.

Vor der Einführung des neuen Medikamentes „SchmerzAde“ sollst Du testen, ob Nebenwirkungen dieses Medikaments bei höchstens einem Prozent der Patienten beobachtet werden können.

In welche Richtung Du die Hypothesen beim einseitigen Test formulierst, hängt nun von den inhaltlichen Gegebenheiten ab.

Arten von Fehlern

Mit jedem Test sind zwei Arten von Fehlern verbunden,

  • Du verwirfst die Nullhypothese irrtümlich, obwohl sie zutrifft (Fehler 1. Art).
  • Du behältst die Nullhypothese bei, obwohl sie nicht zutrifft (Fehler 2. Art).

Nur den Fehler erster Art kannst Du mit dem Signifikanzniveau α kontrollieren. Deshalb solltest Du die Nullhypothese immer negativ zu der Hypothese formulieren, deren Zutreffen Du vermutest.

In obigem Beispiel nimmst Du an, dass „SchmerzAde“ bei weniger als 1% der Probanden Nebenwirkungen hervorruft. Die Nullhypothese formulierst Du negativ zu dieser Aussage als

    \begin{equation*} H_0:p\geq1\% \quad \text{gegen} \quad H_1:p< 1\% \end{equation*}

.

Wird die Nullhypothese verworfen (was Du aus Sicht des Herstellers vermutest und hoffst), so ist die Wahrscheinlichkeit eines Fehlers 1. Art mit dem Signifikanzniveau von α bestimmt.

Wieso die Unterscheidung?

Grundsätzlich könntest Du auch auf die Idee kommen, immer zweiseitig testen zu wollen, nach dem Motto „sicher ist sicher“. Wenn Du aber sowieso schon weißt, dass Dich nur eine Richtung der Abweichung interessiert, kannst Du den kritischen Bereich zum Ablehnen der Nullhypothese komplett auf die „interessante“ Seite der Verteilung legen. Inhaltlich erhält Dein Test dadurch eine größere Sicherheit.
Das lässt sich für einen Test bezüglich der Mittelwerte der Grundgesamtheit sehr einfach grafisch darstellen.

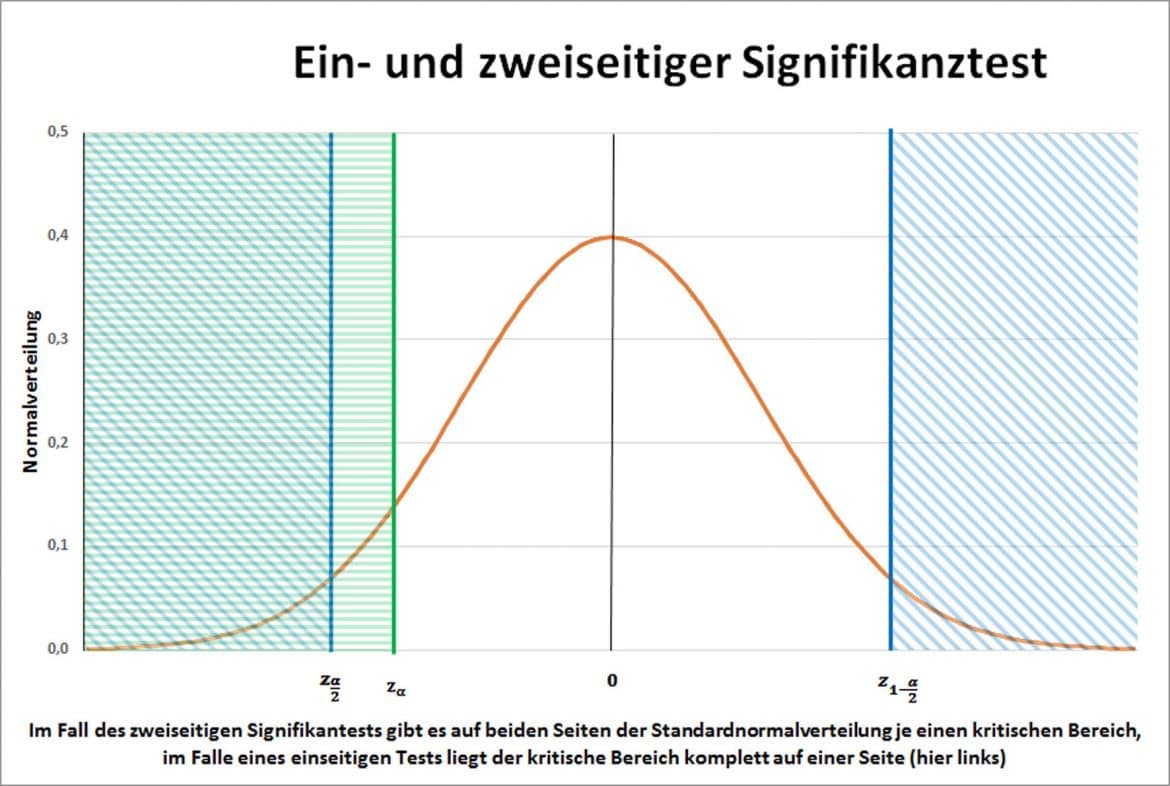
signifikanztest-vergleich

In der Grafik siehst Du die beiden kritischen Teilbereiche für den zweiseitigen Signifikanztest blau schraffiert. Sie beginnen an den Achsenwerten z_{\alpha/2} und z_{1-\alpha/2}. Grün schraffiert ist der kritische Bereich für Deinen einseitigen Test. Er beginnt bei z_{\alpha}.

Ist Deine Prüfgröße kleiner als z_{\alpha/2}, so ergeben beide Tests das gleiche Ergebnis, die Nullhypothese zu verwerfen. Ist die Prüfgröße dagegen größer als z_{\alpha} und kleiner als z_{1-\alpha/2}, entscheiden auch die beiden Tests einheitlich und verwerfen die Nullhypothese nicht.

Liegt dagegen Deine Prüfgröße zwischen und z_{1-\alpha/2} und z_{\alpha}, so führt der einseitige Test zum Verwerfen der Nullhypothese, der zweiseitige Test nicht. Du kannst daraus erkennen, dass der einseitige Test für Abweichungen an einer bekannten Seite der Verteilung „schärfer“ ist.