p-Wert, kritischer Wert

Der kritische Wert trennt den Annahmebereich eines statistischen Tests von seinem Ablehnungsbereich oder auch kritischen Bereich ab.

Grundsätzlich gehst Du davon aus, dass Deine Stichprobenergebnisse Realisationen von Zufallsvariablen darstellen, die sich aus den Parametern der Grundgesamtheit und Zufallseinflüssen zusammensetzen. Bezüglich der Parameter der Grundgesamtheit stellst Du nun eine Vermutung an und formulierst daraus Deine Nullhypothese.

Unter der Voraussetzung, dass die Nullhypothese stimmt, folgen die Realisationen der Stichprobe einer bekannten Verteilungsfunktion. Du kannst dann bestimmen, mit welcher Wahrscheinlichkeit Deine Realisation der Stichprobe kleiner oder gleich einem betrachteten Wert ist.

Was ist der kritische Wert?

Als kritischen Wert bestimmst Du nun im Fall eines gerichteten Tests denjenigen Wert, unterhalb bzw. oberhalb der Stichprobenrealisationen liegen, falls die Nullhypothese gilt.

Angenommen, für die normalverteilte Zufallsvariable „Körpergröße von Frauen“ mit bekannter Varianz hast Du eine Stichprobe erhoben. Du hast als nächstes den Mittelwert der Stichprobe berechnet und möchtest mit einer Irrtumswahrscheinlichkeit von die Hypothese testen, die Körpergröße von Frauen sei im Schnitt niedriger als ein im Internet angegebener Wert :

   

Der Stichprobenmittelwert folgt laut Problemstellung einer –
Normalverteilung, deren Dichtefunktion standardisiert durch die braune Funktion in der Grafik dargestellt ist:

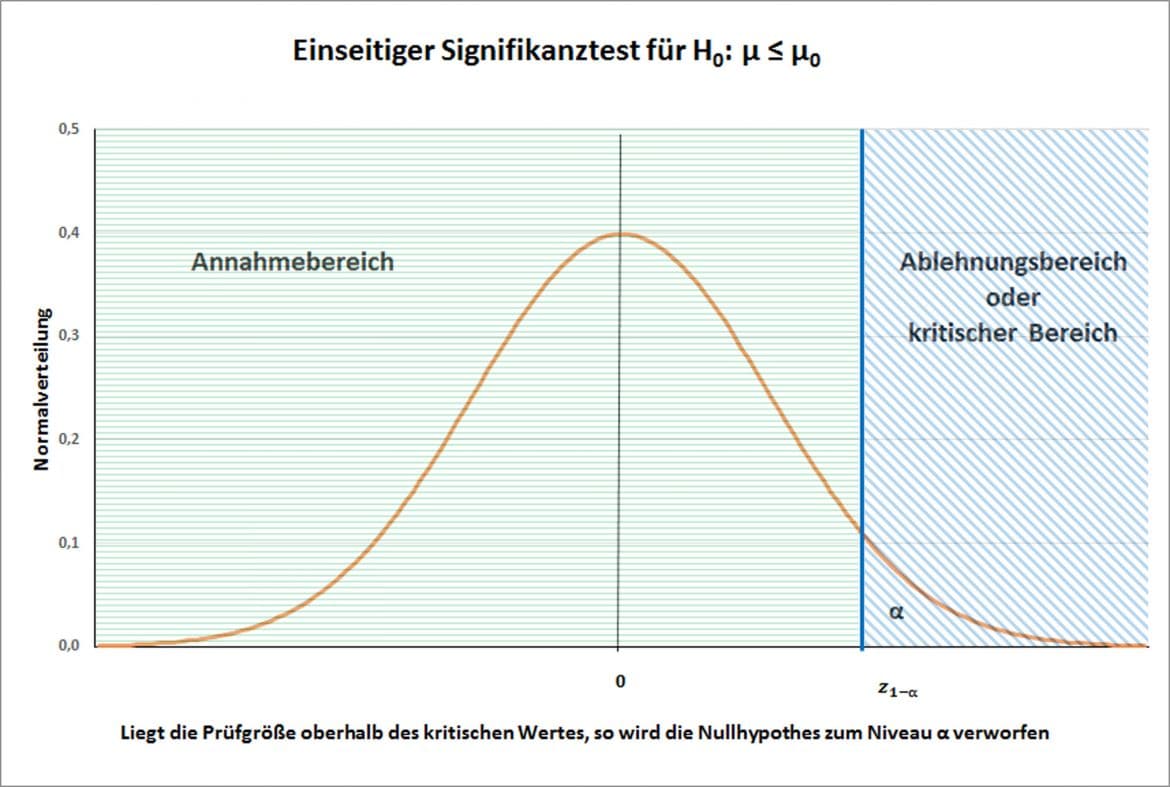
Die Gesamtfläche unter der Dichtefunktion der Standardnormalverteilung ergibt 1: Mit einer Wahrscheinlichkeit von 100% nimmt der standardisierte Stichprobenmittelwert irgendeinen Wert an.

Annahmebereich und Ablehnungsbereich

Als ermittelst Du als denjenigen standardisierten Wert, unterhalb dessen der Stichprobenmittelwert bei Gelten der Nullhypothese mit einer Wahrscheinlichkeit von 95% liegt. Der Annahmebereich Deines Testes, der in der Grafik grün schraffiert eingezeichnet ist, enthält alle standardisierten Werte, die kleiner oder gleich sind als . Der Bereich wird also durch das Intervall dargestellt. Der Ablehnungsbereich, in der Grafik blau schraffiert, enthält alle standardisierten Werte, die größer sind als , und lässt sich als das Intervall beschreiben.

Ist Deine Prüfgröße, im Beispiel die standardisierte mittlere Körpergröße, größer als der ermittelte kritische Wert, so fällt sie in den Ablehnungsbereich. In diesem kritischen Bereich verwirfst Du die Nullhypothese.

Ist Deine Prüfgröße dagegen kleiner als der ermittelte Wert, so liegt Dein Testergebnis im Annahmebereich. Jetzt verwirfst Du die Nullhypothese nicht. Da man empirische Hypothesen nur falsifizieren, nicht aber verifizieren kann, kannst Du daraus nicht schließen, dass sie gilt. Der Test besagt in diesem Fall nur, dass die ermittelten Stichprobenwerte nicht gegen Deine Hypothese sprechen.

Im Fall einer entgegengesetzt formulierten Nullhypothese, die Körpergröße sei größer oder gleich als ein betrachteter Wert, erfolgt die Entscheidung entsprechend auf der anderen Seite der Verteilung: Deinen kritischen Wert ermittelst Du dann als . Das ist der standardisierte Wert, unterhalb dem der Stichprobenmittelwert bei Gelten der Nullhypothese mit einer Wahrscheinlichkeit von 5% liegt.

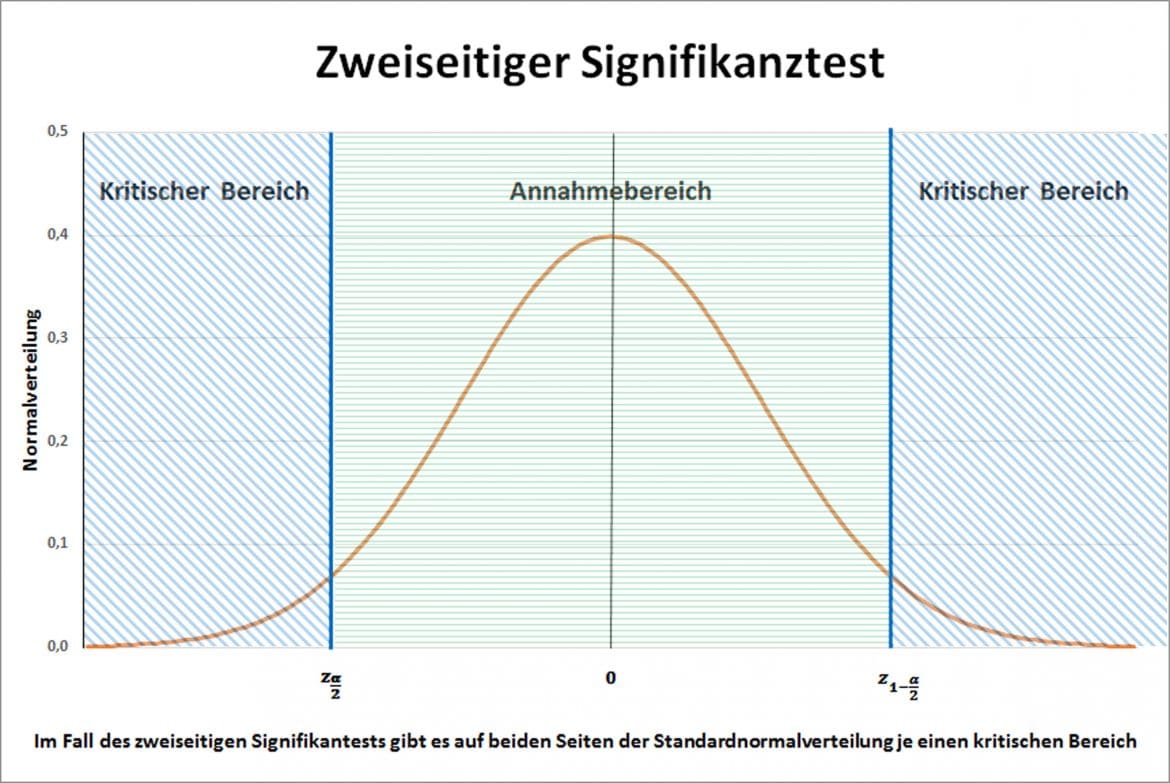
Zweiseitiges Testen

Im Fall eines ungerichteten Tests lauten Deine Hypothesen:

   

Intuitiv einleuchtend ist: Je mehr das Stichprobenergebnis im Zentrum der Verteilung liegt, desto eher spricht die Stichprobe für ein Nichtverwerfen der Hypothese ; je mehr es am äußeren Rand der Verteilung liegt, desto wahrscheinlicher ist es, dass nicht zutrifft. Alpha bestimmt folglich genau die kritischen Werte, bei deren Überschreiten die Entscheidung gegen die Nullhypothese fällt.

   

Die Grafik zeigt den Annahmebereich des Tests im Zentrum der Verteilung grün schraffiert. Der kritische Bereich oder Ablehnungsbereich ist symmetrisch auf die beiden Ränder der Verteilung aufgeteilt und ist blau schraffiert in der Grafik zu erkennen.

Im Gegensatz zur bisher skizzierten klassischen Durchführung der Testentscheidung hat sich mit Aufkommen leistungsstarker Rechner eine zweite Variante entwickelt, die grundsätzlich auf den gleichen Überlegungen beruht, aber den p-Wert des Testergebnisses ermittelt:

Was ist der p-Wert?

Der p-Wert gibt an, wie wahrscheinlich es unter der Nullhypothese ist, das aktuelle Ergebnis oder ein extremeres zu erhalten, bei welchem Wert von α also dieses Stichprobenergebnis Dein kritischer Wert wäre. Die Testentscheidung triffst Du dann über den Vergleich Deines p-Wertes mit dem vorher festgelegten α. Ist der p-Wert größer als , so wird die Hypothese nicht verworfen; ist er kleiner als α, so wird sie verworfen.

Zur Überprüfung der Körpergröße von Frauen hast Du zwei Stichproben erhoben und daraus als standardisierte mittlere Körpergrößen und berechnet.

Standardisierter Stichprobenmittelwert z	FNV(z)	p-Wert = 1 – FNV(z)	Testentscheidung für α = 0,05
0,76	0,7764	0,2236	p-Wert > α: H0 wird nicht verworfen
2,15	0,9842	0,0158	p-Wert < α: H0 wird verworfen

Der Wert der Standardnormalverteilung an der Stelle 0,76 beträgt 0,7764. Unter der Nullhypothese kann folglich mit einer Wahrscheinlichkeit von 0,2236 = 1- 0,7764 ein extremeres Stichprobenergebnis als 0,76 angenommen werden. Da 0,2236 größer ist als α = 0,05, wird die Nullhypothese nicht verworfen. Die Grafik zeigt diese Situation grün schraffiert an.

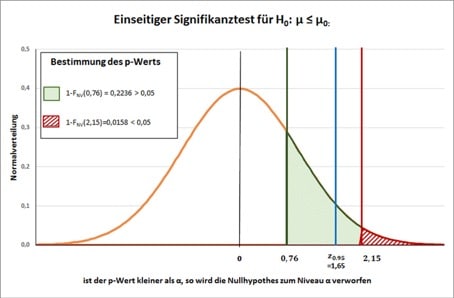
Der Wert der Standardnormalverteilung an der Stelle 2,15 beträgt 0,9842. Unter der Nullhypothese kann mit einer Wahrscheinlichkeit von 0,0158 = 1- 0,9842 ein extremeres Stichprobenergebnis als 2,15 angenommen werden. Da 0,0158 kleiner ist als α = 0,05, wird die Nullhypothese verworfen. Die Grafik zeigt diese Situation rot schraffiert an.