Vierfeldertafel

Vierfeldertafel

  • 26. April 2018
  • Posted by: Mika
Keine Kommentare

Unter einer Vierfeldertafel verstehst Du eine Kontingenztabelle aus zwei binären Merkmalen beliebigen Skalenniveaus, die also beide nur zwei Ausprägungen haben. Du kannst mit der Vierfeldertafel sowohl die absoluten wie die relativen Häufigkeiten darstellen, die Stärke des Zusammenhangs berechnen und testen, ob die beiden Merkmale unabhängig sind.

Du möchtest beispielsweise wissen, ob die Wartezeit von Patienten in einer Praxis von deren Krankenversicherung abhängig ist.

Dazu notierst Du bei den n=26 Patienten, die an einem Tag in einer Arztpraxis behandelt werden, die Realisationen des Merkmals X: Versicherung mit den Ausprägungen (X=1: Kassenpatient und X=2: Privatpatient) und die Wartezeit Y (Y=1: maximal 30 Minuten und Y=2: mehr als 30 Minuten).

Aus Deinen Aufzeichnungen kannst Du eine Vierfeldertafel mit absoluten Häufigkeiten erstellen, indem Du in die möglichen Merkmalsausprägungen von X in die Zeilen, die von Y in die Spalten schreibst und die vier Felder mit den beobachteten Häufigkeiten füllst:

Absolute Häufigkeiten n_{ij} Y: Wartezeit Summe
kurze Wartezeit lange Wartezeit
Y=1 Y=2
X:
Krankenversicherung. 		PKV X=1 n_{11}=3 n_{12}=1 n_{1 cdot}=4
GKV X=2 n_{21}=10 n_{11}=12 n_{2 cdot}=22
Summe n_{cdot 1}=13 n_{cdo 2t}=13 n=26

Die n_{i \cdot} und n_{\cdot j} stellen die Randhäufigkeiten dar, mit denen die i-te Ausprägung von X bzw. die j-te Ausprägung von Y beobachtet wurde.
In der Grafik sind die Zahlen der Tabelle dargestellt:

Vierfeldertafel

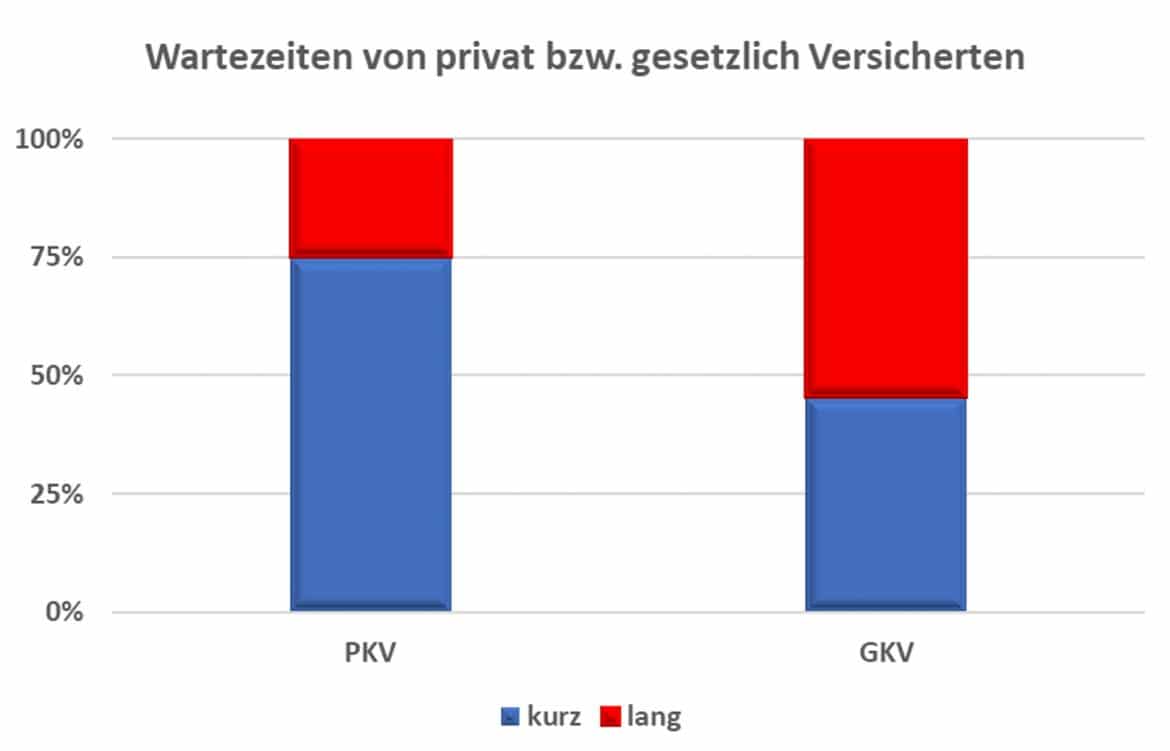
Dividierst Du alle absoluten Häufigkeiten durch die Zahl der Beobachtungen, so erhältst Du die Vierfeldertafel mit relativen Häufigkeiten:

Relative Häufigkeiten

h_{ij}=\frac { n_{ij}} n		 Y: Wartezeit Summe
kurze Wartezeit lange Wartezeit
Y=1 Y=2
X:
Krankenversicherung.		 PKV X=1 h_{11}=0,1154 h_{12}=0,0385 h_{1 \cdot}=0,1538
GKV X=2 h_{21}=0,3846 h_{11}=0,4615 h_{2 \cdot}=0,8462
Summe h_{\cdot 1}=0,5 h_{\cdo 2t}=0,5 h=26

Die relativen Häufigkeiten h_{ij} kannst Du als Schätzwerte \hat p_{ij} für die Wahrscheinlichkeiten annehmen, mit denen die Merkmalskombinationen auftreten;

    \begin{equation*} \hat p_{ij} = h_{ij}, \quad f\"ur \nobreakspace i,j =0 \nobreakspace und \nobreakspace 1 \end{equation*}

Die Randhäufigkeiten sind dann Schätzwerte für die Wahrscheinlichkeiten, mit denen die Ausprägungen von X und Y eintreten, ohne dass die Ausprägung des anderen Merkmals bekannt ist.

    \begin{equation*} \hat P(X=1) = h_{1 \cdot}, \nobreakspace \hat P(X=2) = h_{2 \cdot}\end{equation*}

und

    \begin{equation*} \hat P(Y=1) = h_{\cdot 1}\nobreakspace und \nobreakspace \hat P(Y=2) = h_{\cdot 2} \end{equation*}

Falls X und Y unabhängig voneinander sind, müsste gelten:

    \begin{equation*} p^*_{ij}=\hat P[(X=i) \nobreakspace und \nobreakspace (Y=j)] = P(X=i) \cdot P(Y=j) \end{equation*}

Die unter Unabhängigkeit zu erwartenden Anzahlen erhältst Du dann als n^*_{ij}=n \cdot p^*{ij}.
Für Dein Beispiel ergibt sich:

unter Unabhängigkeit von X und Y zu erwartende Anzahlen
n^*_{ij}=n \cdot p^*_{ij}		 Y: Wartezeit
kurze Wartezeit lange Wartezeit
Y=1 Y=2
X:
Krankenversicherung.		 PKV X=1 n^*_{11}=2 n^*_{12}=2 n_{1 \cdot}=4
GKV X=2 n^*_{21}=11 n^*_{11}=11 n_{2 \cdot}=22
n_{\cdot 1}=13 n_{\cdo 2t}=13 h=26

Je stärker sich jetzt die n^*_{ij} von den \n_{ij} unterscheiden, desto größer ist der Zusammenhang und damit die Abhängigkeit der beiden Merkmale X und Y.
Daraus kannst Du etwa den Chi-Quadrat- oder Kontingenzkoeffizienten Deiner Vierfeldertafel berechnen als Summe der quadratischen Abweichungen, normiert durch die geschätzten Anzahlen:

    \begin{equation*} \chi^2 = \sum_{i=1}^2 \sum_{j=0}^2 \frac {(n_{ij} - n^*_{ij})^2}{n^*_{ij}}=1,1818 \end{equation*}

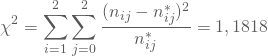
\chi^2 ist \chi^2-verteilt mit \nu=((2-1)\cdot(2-1))=1 Freiheitsgraden. Du kannst daher die Hypothesen

H_0: X und Y sind unabhängig

gegen

H_1: X und Y sind nicht unabhängig

testen.

Der Vergleich von \chi^2 mit dem kritischen Wert zum Niveau von 5\% bei einem Freiheitsgrad führt nicht zum Verwerfen der Nullhypothese von Unabhängigkeit.

    \begin{equation*} \chi^2_{pr} = 1,1818 < 3,8405= \chi^2_{0,95}(1)\end{equation*}

Als Zusammenhangsmaß ist \chi^2 nicht geeignet, da es nicht auf das Intervall [0;1] beschränkt ist; Du berechnest daher Pearsons C,

    \begin{equation*} C = \sqrt{\frac {\chi^2}{\chi^2+n}}=\sqrt{\frac {1,1818}{1,1818+26}}=0,2085\end{equation*}

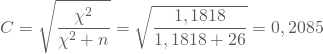
und normierst diese Kennzahl auf das Intervall [0;1], indem Du durch C_{max}= \sqrt{\frac {1} 2}=0,7071 dividierst, durch den Wert, den C maximal annehmen kann:

Du erhältst den korrigierten Kontingenzkoeffizienten als:

    \begin{equation*} C_{korr}=\frac C {C_{max}}= \frac {0,2085} {0,7071}= 0,2949\end{equation*}

Der Wert des korrigierten Kontingenzkoeffizienten Deiner Vierfeldertafel weist auf einen geringen Zusammenhang zwischen der Wartezeit von Patienten und ihrer Versicherung hin.