Rangkorrelation nach Spearman

Rangkorrelation nach Spearman

  • 26. Januar 2017
  • Posted by: Mika
Keine Kommentare

Dieser Artikel erklärt das Thema Rangkorrelation. Der Korrelationskoeffizient nach Bravais-Pearson ist einfach auszurechnen und eine verbreitete Kenngröße. Allerdings benötigt man die engen Voraussetzungen eines linearen Zusammenhangs und der Normalverteilung in der Grundgesamtheit sowie metrisches Datenmaterial.

Falls diese Voraussetzungen nicht gegeben sind, ist der Spearman´sche Rangkorrelationskoeffizient eine brauchbare Alternative. Du benötigst keine Annahmen über die Verteilung der Variablen und bist nicht auf lineare Zusammenhänge beschränkt. Damit ist Dein Anwendungsgebiet für diesen Koeffizienten deutlich größer als das des Korrelationskoeffizienten nach Bravais-Pearson.

Der Spearman’sche Rangkorrelationskoeffizient

Der Koeffizient ist konzeptionell aufgebaut wie der Korrelationskoeffizient, verwendet aber anstelle der Stichprobenrealisationen der Variablen deren Ränge. Damit lautet er:

    \begin{equation*} \rho_s = \frac {cov(rg(X),rg(Y))} { \sigma_{rg(X)} \cdot \sigma _{rg(Y)}} \end{equation*}

Als Fußballfan interessiert es Dich beispielsweise zu überprüfen, ob die Höhe der Netto-Transferausgaben, die die Vereine für neue Spieler ausgeben, in Zusammenhang mit deren Rangliste in der Bundesliga stehen. Daher stellst Du die folgende Tabelle auf. Die Zahlen in der dritten Spalte sind allerdings erfunden und hier von rein methodisch-statistischem Interesse. Du bestimmst dann für beide Zufallsvariablen den Rang der Beobachtungen.

Bindungen bedeutet, dass gleiche Werte mehrmals beobachtet werden. Im Falle von Bindungen bildest Du den Mittelwert aus den in Frage kommenden Rängen. Zum Beispiel haben sowohl Mönchengladbach als auch der VfL Wolfsburg 1,4 Millionen Transferausgaben gezahlt. Beide gemeinsam belegen daher die Ränge 11 und 12. Du berücksichtigst die Gleichheit der Ränge, indem Du die in Frage kommenden Rangwerte mittelst und beiden den Rangwert 11,5 zuweist. Analoges gilt für RB Leipzig und Eintracht Frankfurt, die beide 2,8 Millionen Transferausgaben gezahlt haben. Beiden wird der Rangwert 5,5 zugewiesen.

Name des Vereins rg(X):
Rang in der 
Bundesliga		 Y:
Transferausgaben
in Mio		 rg(Y):
Rang bezüglich der Transferausgaben
FC Bayern München 1 5,7 1,0
Dortmund 2 3,9 3,0
1. FC Köln 3 4,3 2,0
Mönchengladbach 4 1,4 11,5
Eintracht Frankfurt 5 2,8 5,5
Hertha BSC 6 2,4 7,0
RB Leipzig 7 2,8 5,5
1. FSV Mainz 8 3,7 4,0
1899 Hoffenheim 9 1,0 14,0
Bayer 04 Leverkusen 10 0,7 15,0
FC Augsburg 11 0,5 16,5
FC Freiburg 12 1,8 9,0
VfL Wolfsburg 13 1,4 11,5
SV Darmstadt 98 14 1,7 10,0
SV Werder Bremen 15 1,9 8,0
Hamburger SV 16 0,5 16,5
FC Ingolstadt 04 17 1,1 13,0
FC Schalke 04 18 0,2 18,0

Der Schätzwert

Als Schätzwert für \rho_s setzt Du erwartungstreue Schätzer für Kovarianz und Varianzen ein und erhältst als Schätzwert:

    \begin{equation*} r_s= \frac {cov(rg_x,rg_y)} { s_{rg_x} \cdot s_{rg_y}} = \frac{\displaystyle \frac 1 {n-1} \sum_{i=1}^n {(rg(x_i)-\bar {rg}(x)) \cdot (rg(y_i)- \bar {rg}_y)}}{\sqrt { \frac 1 {n-1} { \displaystyle \sum_{i=1}^n (rg(x_i)-\bar {rg}(x))^2}}\cdot \sqrt { \frac 1 {n-1} { \displaystyle \sum_{i=1}^n (rg(x_i)-\bar {rg}(x))^2}} }\end{equation*}

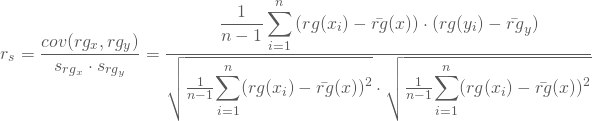
Einsetzen der Zahlen ergibt für Dein Beispiel einen Wert von r_s=0,741. Der Zusammenhang zwischen dem Rang des Vereins und der Höhe der Transferausgaben beträgt also nach dem Spearman´schen Rangkorrelationskoeffizienten etwa 74\%.
Möchtest Du jetzt testen, ob das wahre \rho_s der Grundgesamtheit signifikant von Null verschieden ist, so formulierst Du Deine Hypothesen:

    \begin{equation*} H_0: \rho_s =0 \quad gegen \quad H_1: \rho_s \ne 0\end{equation*}

Der Test wird analog zum Test des Korrelationskoeffizienten auf Signifikanz durchgeführt. Du vergleichst demnach die t-verteilte Prüfgröße mit dem kritischen t-Wert zum Niveau (1- \alpha/2) bei (n-2) Freiheitsgraden. Mit

    \begin{equation*} t_{pr} = \frac {r \cdot \sqrt {n-2}} { \sqrt {1-r^2}} =\frac {(0,741) \cdot \sqrt {16}} { \sqrt {1-(0,741)^2}} = 4,415 > 2,1199 = t_{(0,975;16)}} \end{equation*}

kannst Du folglich die Nullhypothese verwerfen und schließt auf einen signifikanten Zusammenhang mit einer Irrtumswahrscheinlichkeit von 5\%.