Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Scheinkorrelation / partielle Korrelation
- 26. Januar 2017
- Posted by: Mika
Von Scheinkorrelation spricht man, wenn Zufallsvariablen hoch miteinander korreliert sind, obwohl kein Kausalzusammenhang zwischen ihnen besteht. Der Zusammenhang ist dann statistisch signifikant. Man spricht auch von partieller Korrelation. Der Grund ist meist der, dass beide Variablen von einer dritten Variablen gleichermaßen beeinflusst werden.
Beispiel für eine Scheinkorrelation
Nach einem großen Familiensportfest analysierst Du beispielsweise die Ergebnisse der Wettkampfteilnehmer. Dabei stellst Du fest, dass ein erstaunlich hoher positiver Zusammenhang zwischen dem Gewicht G der Teilnehmer und der Sprungweite S besteht. Du berechnest den Korrelationskoeffizienten von Sprungweite und Gewicht zu ![]() = 0,81 und prüfst ihn auf Signifikanz, die auch gegeben ist.
= 0,81 und prüfst ihn auf Signifikanz, die auch gegeben ist.
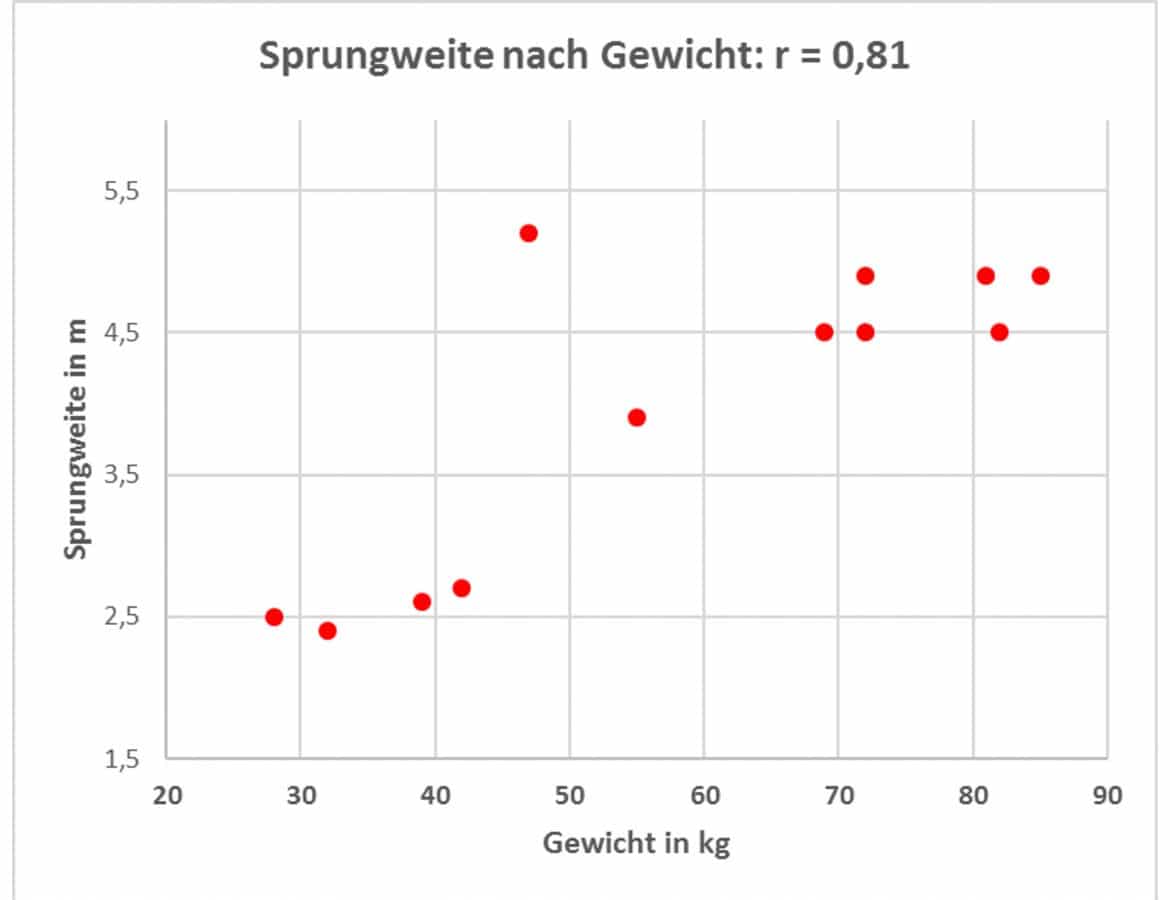
Die Grafik zeigt den Zusammenhang deutlich.
Bisher warst Du ganz selbstverständlich davon ausgegangen, dass leichte Menschen weiter springen können. Nach einigem Überlegen kommt Dir die Idee, dass Gewicht und Sprungweite durch die Variable K Köpergröße beeinflusst werden. Je größer ein Mensch ist, desto schwerer ist er in der Regel auch. Aber desto weiter kann er unter sonst gleichen Bedingungen auch springen.
Die grafische Gegenüberstellung der Variablen zeigt sofort, dass diese beiden Zusammenhänge in Deiner Stichprobe gegeben sind.
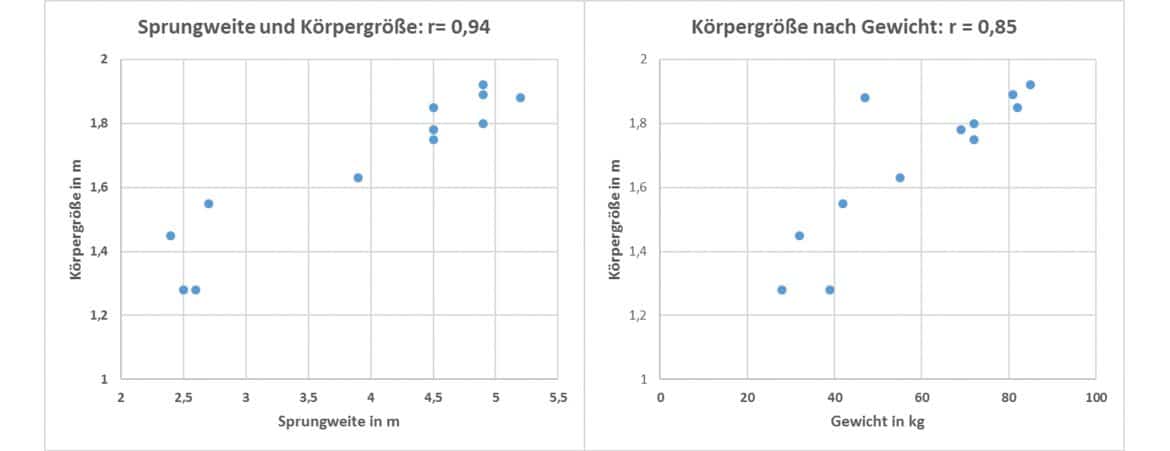
Daher berechnest Du nun zusätzlich die Korrelationskoeffizienten ![]() von Gewicht und Körpergröße einerseits und
von Gewicht und Körpergröße einerseits und ![]() von Sprungweite und Körpergröße anderseits zu
von Sprungweite und Körpergröße anderseits zu ![]() und
und ![]() .
.
Wie rechnet man den Einfluss einer Drittvariable heraus?
Du suchst jetzt nach einem Korrelationsmaß, das den Einfluss der Körpergröße aus der Korrelation zwischen Sprungweite und Gewicht herausrechnet. Der partielle Korrelationskoeffizient ![]() ist definiert als Korrelationskoeffizient von G und S, korrigiert um den Zusammenhangseffekt von Körpergröße auf Gewicht und Sprungweite. Zusätzlich wird er noch normiert mit der nicht durch die dritte Variable K erklärte Streuung von G und S.
ist definiert als Korrelationskoeffizient von G und S, korrigiert um den Zusammenhangseffekt von Körpergröße auf Gewicht und Sprungweite. Zusätzlich wird er noch normiert mit der nicht durch die dritte Variable K erklärte Streuung von G und S.
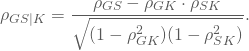
Setzt Du in diese Formel die Stichprobenschätzwerte ![]() ein, so erhältst Du als Schätzwert für die partielle Korrelation zwischen Gewicht und Sprungweite:
ein, so erhältst Du als Schätzwert für die partielle Korrelation zwischen Gewicht und Sprungweite:
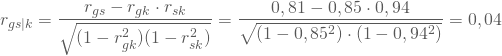
Nachdem Du den Einfluss von Körpergröße auf Gewicht und Sprungweite herausgerechnet hast, besteht ein geringer positiver Zusammenhang zwischen Gewicht und Sprungweite. Dieser Zusammenhang passt mit den Erwartungen Deines gesunden Menschenverstandes eher zusammen.
Um festzustellen, ob der ermittelte Wert des Korrelationskoeffizienten signifikant von Null verschieden ist, wird der übliche Test des Korrelationskoeffizienten auf signifikante Abweichungen von Null durchgeführt. Statistikprogrammsysteme geben neben dem Wert des Koeffizienten den zugehörigen p-Wert an, den Du mit Deinem vorher bestimmen ![]() vergleichst, meistens ist das
vergleichst, meistens ist das ![]() .
.
Ist p > ![]() , kannst Du keinen signifikanten Unterschied von Null feststellen, anderenfalls schließt Du auf einen existierenden Zusammenhang.
, kannst Du keinen signifikanten Unterschied von Null feststellen, anderenfalls schließt Du auf einen existierenden Zusammenhang.
