Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Kreuztabelle / Kontingenztafel
- 26. Januar 2017
- Posted by: Mika
Eine Kreuztabelle oder Kontingenztafel ist eine zweidimensionale Gegenüberstellung der Häufigkeiten von zwei Merkmalen X und Y. Es gibt dabei n bzw. m Ausprägungen, die beliebiges Skalenniveau aufweisen dürfen.
Als Maß für den Zusammenhang beider Merkmale kannst Du den Kontingenzkoeffizienten, auch ![]() -Koeffizienten genannt, berechnen. Anschließend testest Du damit, ob die beiden Variablen unabhängig voneinander sind oder ob ein Zusammenhang zwischen ihnen besteht.
-Koeffizienten genannt, berechnen. Anschließend testest Du damit, ob die beiden Variablen unabhängig voneinander sind oder ob ein Zusammenhang zwischen ihnen besteht.
Vor den Landtagswahlen in den Bundesländern Baden-Württemberg ![]() und Rheinland-Pfalz
und Rheinland-Pfalz ![]() wurde in beiden Ländern repräsentative Umfragen bei je 1000 Personen durchgeführt, welche Partei Y sie wählen würden, „…falls am Sonntag Wahl wäre“. Die Häufigkeiten
wurde in beiden Ländern repräsentative Umfragen bei je 1000 Personen durchgeführt, welche Partei Y sie wählen würden, „…falls am Sonntag Wahl wäre“. Die Häufigkeiten ![]() , mit denen im Land
, mit denen im Land ![]() die Partei
die Partei ![]() angegeben wurde, sind im Inneren der Tabelle dargestellt. Am Rand findest Du die Häufigkeiten
angegeben wurde, sind im Inneren der Tabelle dargestellt. Am Rand findest Du die Häufigkeiten ![]() als Anzahl der Befragten aus dem Bundesland
als Anzahl der Befragten aus dem Bundesland ![]() bzw.
bzw. ![]() als Häufigkeit, mit der die Partei
als Häufigkeit, mit der die Partei ![]() insgesamt genannt wurde:
insgesamt genannt wurde:
| Erhobene Daten |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| CDU | SPD | Grüne | AfD | FDP | Linke | Sonstige | Summe | ||
| Baden- Württemberg | 302 | 120 | 323 | 108 | 80 | 37 | 30 | 1.000 | |
| Rheinland- Pfalz | 358 | 347 | 62 | 109 | 64 | 41 | 19 | 1.000 | |
| Summe | 660 | 467 | 385 | 217 | 144 | 78 | 49 | 2.000 | |
Die Grafik zeigt die erhobenen Werte:
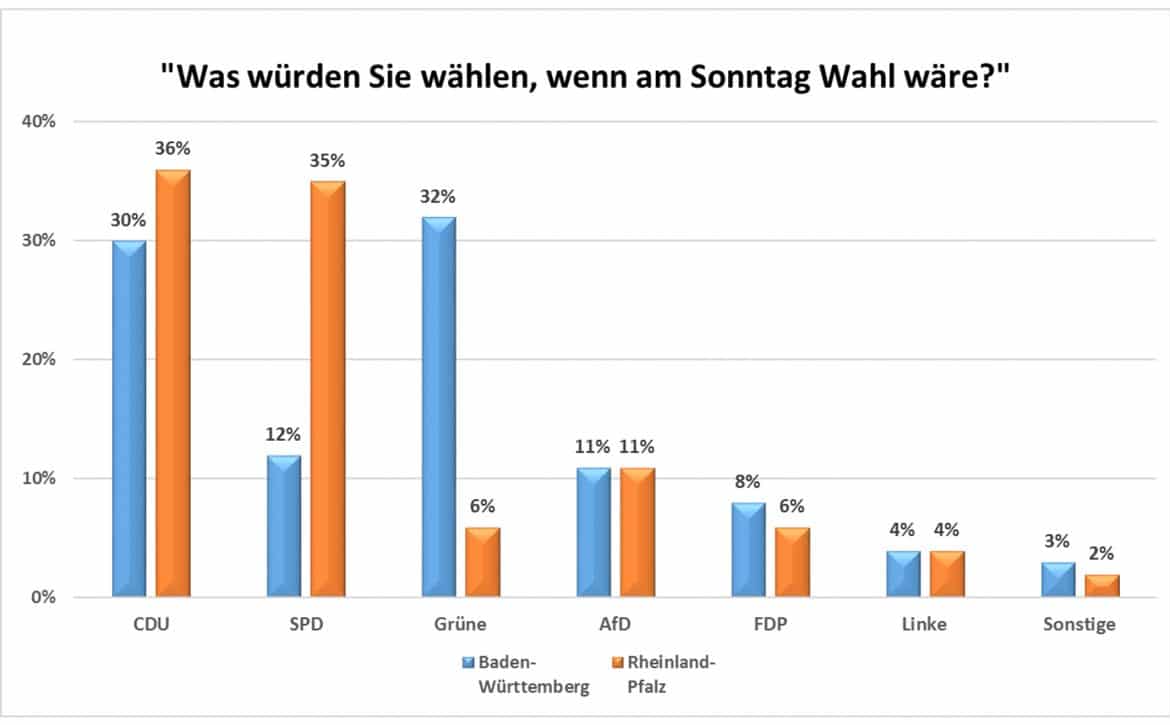
Wie stark beeinflusst die Landeszugehörigkeit die Wahlentscheidung?
Aus diesen Daten möchtest Du analysieren, ob und wie stark die Wahlentscheidung der Bürger durch ihre Landeszugehörigkeit beeinflusst wird. Dazu berechnest Du ein Maß für den Zusammenhang der beiden Merkmale.
Du betrachtest die Wahrscheinlichkeiten ![]() , im Bundesland
, im Bundesland ![]() für die Partei
für die Partei ![]() zu votieren und vergleichst sie mit den Einzelwahrscheinlichkeiten
zu votieren und vergleichst sie mit den Einzelwahrscheinlichkeiten ![]() , im Bundesland
, im Bundesland ![]() zu wohnen sowie
zu wohnen sowie ![]() , die Partei
, die Partei ![]() zu wählen.
zu wählen.
Relative Häufigkeiten als Schätzwerte
Als Schätzwerte für diese Wahrscheinlichkeiten können die relativen Häufigkeiten dienen, so dass:
![]()
Falls ein Zusammenhang zwischen X und Y besteht, ist es für die Wahlentscheidung eines Bürgers bedeutsam, in welchem Bundesland er wohnt.
Falls die Merkmale X: „Bundesland“ und Y: „Partei“ dagegen unabhängig voneinander sind, ist die Wahrscheinlichkeiten für die Entscheidung, ![]() zu wählen, nicht davon abhängig, in welchem Land
zu wählen, nicht davon abhängig, in welchem Land ![]() die Umfrage stattfindet und umgekehrt. Die bedingten Wahrscheinlichkeiten, für
die Umfrage stattfindet und umgekehrt. Die bedingten Wahrscheinlichkeiten, für ![]() zu stimmen, vorausgesetzt man wohnt im Land
zu stimmen, vorausgesetzt man wohnt im Land ![]() , sind dann gleich den Einzelwahrscheinlichkeiten:
, sind dann gleich den Einzelwahrscheinlichkeiten:
![]()
Dann kannst Du die Wahrscheinlichkeit ![]() für das Auftreten der Kombination der Merkmalsausprägungen
für das Auftreten der Kombination der Merkmalsausprägungen ![]() und
und ![]() als Produkt der Einzelwahrscheinlichkeiten darstellen:
als Produkt der Einzelwahrscheinlichkeiten darstellen:
![]()
Setzt Du in diese Formel die Schätzwerte ![]() und
und ![]() ein und multiplizierst die Wahrscheinlichkeiten mit der Gesamtzahl n der Beobachtungen, so erhältst Du Schätzwerte
ein und multiplizierst die Wahrscheinlichkeiten mit der Gesamtzahl n der Beobachtungen, so erhältst Du Schätzwerte ![]() für die zu erwartende Anzahl von Stimmen, falls kein Zusammenhang zwischen X und Y bestehen würde:
für die zu erwartende Anzahl von Stimmen, falls kein Zusammenhang zwischen X und Y bestehen würde:
![]()
Theoretische Kontingenztabelle, falls kein Zusammenhang besteht
Damit kannst Du eine zweite Kontingenztabelle mit Schätzwerten ![]() erstellen. Sie geben Dir an, mit welchen Häufigkeiten Du rechnen könntest, falls kein Zusammenhang zwischen den Variablen X und Y bestünde:
erstellen. Sie geben Dir an, mit welchen Häufigkeiten Du rechnen könntest, falls kein Zusammenhang zwischen den Variablen X und Y bestünde:
| Geschätzte Daten |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| CDU | SPD | Grüne | AfD | FDP | Linke | Sonstige | Summe | ||
| Baden- Württemberg | 330 | 234 | 193 | 109 | 72 | 39 | 25 | 1.000 | |
| Rheinland- Pfalz | 330 | 234 | 193 | 109 | 72 | 39 | 25 | 1.000 | |
| Summe | 660 | 467 | 385 | 217 | 144 | 78 | 49 | 2.000 | |
Du hast damit für jede Kombination von X und Y zum einen die beobachtete Häufigkeit ![]() sowie eine geschätzte Häufigkeit
sowie eine geschätzte Häufigkeit ![]() für den Fall zur Verfügung, dass kein Zusammenhang zwischen den beiden Variablen besteht. Je größer die Unterschiede zwischen
für den Fall zur Verfügung, dass kein Zusammenhang zwischen den beiden Variablen besteht. Je größer die Unterschiede zwischen ![]() und
und ![]() sind, umso mehr sprechen Deine Daten für einen Zusammenhang von X und Y und gegen die Vermutung der Unabhängigkeit.
sind, umso mehr sprechen Deine Daten für einen Zusammenhang von X und Y und gegen die Vermutung der Unabhängigkeit.
Summierst Du jetzt die Summe der quadratischen Abweichungen zwischen ![]() und
und ![]() , zur Normierung dividiert durch
, zur Normierung dividiert durch ![]() , so erhältst Du die quadratische Kontingenz
, so erhältst Du die quadratische Kontingenz ![]() Deiner Daten:
Deiner Daten:
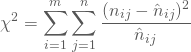
Der Kontingenzkoeffizient ist ![]() -verteilt mit
-verteilt mit ![]() Freiheitsgraden und Du kannst mit ihm die folgenden Hypothesen testen:
Freiheitsgraden und Du kannst mit ihm die folgenden Hypothesen testen:
![]() : Es besteht kein Zusammenhang zwischen dem Bundesland und der Wahlentscheidung für eine Partei.
: Es besteht kein Zusammenhang zwischen dem Bundesland und der Wahlentscheidung für eine Partei.
![]() : Es besteht ein signifikanter Zusammenhang zwischen dem Bundesland und der Wahlentscheidung für eine Partei.
: Es besteht ein signifikanter Zusammenhang zwischen dem Bundesland und der Wahlentscheidung für eine Partei.
Die Testentscheidung
Jetzt setzt Du die Werte Deines Beispiels ein und vergleichst mit dem kritischen Wert bei einer Irrtumswahrscheinlichkeit von ![]() . Mit
. Mit
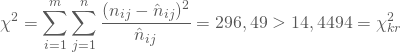
verwirfst Du die Nullhypothese und schließt, dass ein signifikanter Zusammenhang zwischen dem Bundesland und der Entscheidung für eine Partei besteht.
Als Maß des Zusammenhangs sagt Dir ![]() allerdings wenig aus, da die Höhe des Kontingenzkoeffizienten stark durch die Anzahl der Merkmalsausprägungen und die Zahl der Beobachtungen beeinflusst wird.
allerdings wenig aus, da die Höhe des Kontingenzkoeffizienten stark durch die Anzahl der Merkmalsausprägungen und die Zahl der Beobachtungen beeinflusst wird.
Daher schlug Pearson folgende Normierung vor:
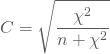
C nimmt maximal den Wert ![]() an, wobei
an, wobei ![]() durch die kleinere Anzahl der Merkmalsausprägungen von X und Y bestimmt wird:
durch die kleinere Anzahl der Merkmalsausprägungen von X und Y bestimmt wird:
![]()
Dividierst Du nun noch C durch ![]() , so erhältst Du einen korrigierter Kontingenzkoeffizient, der auf das Intervall zwischen Null und eins beschränkt ist, wie für Zusammenhangsmaße üblich:
, so erhältst Du einen korrigierter Kontingenzkoeffizient, der auf das Intervall zwischen Null und eins beschränkt ist, wie für Zusammenhangsmaße üblich:
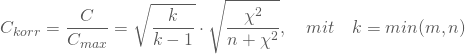
Für Deine Wahluntersuchung ergibt sich ![]() . Das Mass für den Zusammenhang zwischen X und Y in Deiner Untersuchung liegt also knapp über 50 Prozent.
. Das Mass für den Zusammenhang zwischen X und Y in Deiner Untersuchung liegt also knapp über 50 Prozent.
