Kendalls Konkordanzanalyse

Kendalls Konkordanzanalyse ist ein nichtparametrisches statistisches Verfahren, mit dem Du überprüfen kannst, inwieweit die Rangwertungen verschiedener Personen bezüglich einer Reihe von Objekten übereinstimmen. Sie stellt im Fall von 2 Rangwertungen eine Alternative zum Rangkorrelationskoeffizienten dar.

Die Idee der Kendalls Konkordanzanalyse

Idee des Verfahrens ist es, dass Du m Personen, der „Jury“, eine Menge von n Objekten gegenüberstellst und alle Personen die Objekte in eine Rangfolge bringen. Ergebnis Deiner Erhebung sind dann Rangplätze , die den Rangwert des i-ten Objektes aus der Sicht des j-ten Beurteilers darstellen.

Stell Dir beispielsweise vor, Du nimmst als Zuschauer an einem Kochwettkampf teil: Fünf Hobbyköche kreieren ihre persönliche Variante von „Saltimbocca an Rosmarinkartoffeln mit Marktgemüse“ und servieren das Ergebnis der Jury aus vier Gutachtern. Jeder Gutachter probiert dann die fünf Gerichte und bewertet sie eindeutig mit den Plätzen eins bis fünf. Als Ergebnis liegt Dir folgende Tabelle vor:

			Köche: i = 1 bis 5
			1	2	3	4	5
Gutachter j = 1 bis 4			Anne	Horst	Josef	Doris	Franz
	1	Schmid	1	4	2	3	5
	2	Schulz	2	3	4	1	5
	3	Meier	2	4	3	1	5
	4	Müller	4	3	2	1	5
Summe der Rangwerte			9	14	11	6	20

Als nächstes möchtest Du testen, inwieweit die Urteile der Jurymitglieder miteinander übereinstimmen.

Summierst Du die über j, so erhältst Du mit die Summe aller Rangplätze, die das i-te Objekt insgesamt bekommen hat.

Die Grafik zeigt die den Köchen von den einzelnen Jurymitgliedern zugewiesenen Ränge, die Rangplatzsumme als Gesamthöhe der Säule jedes Kochs und als gestrichelte Linie den Mittelwert der fünf Rangplatzsummen.

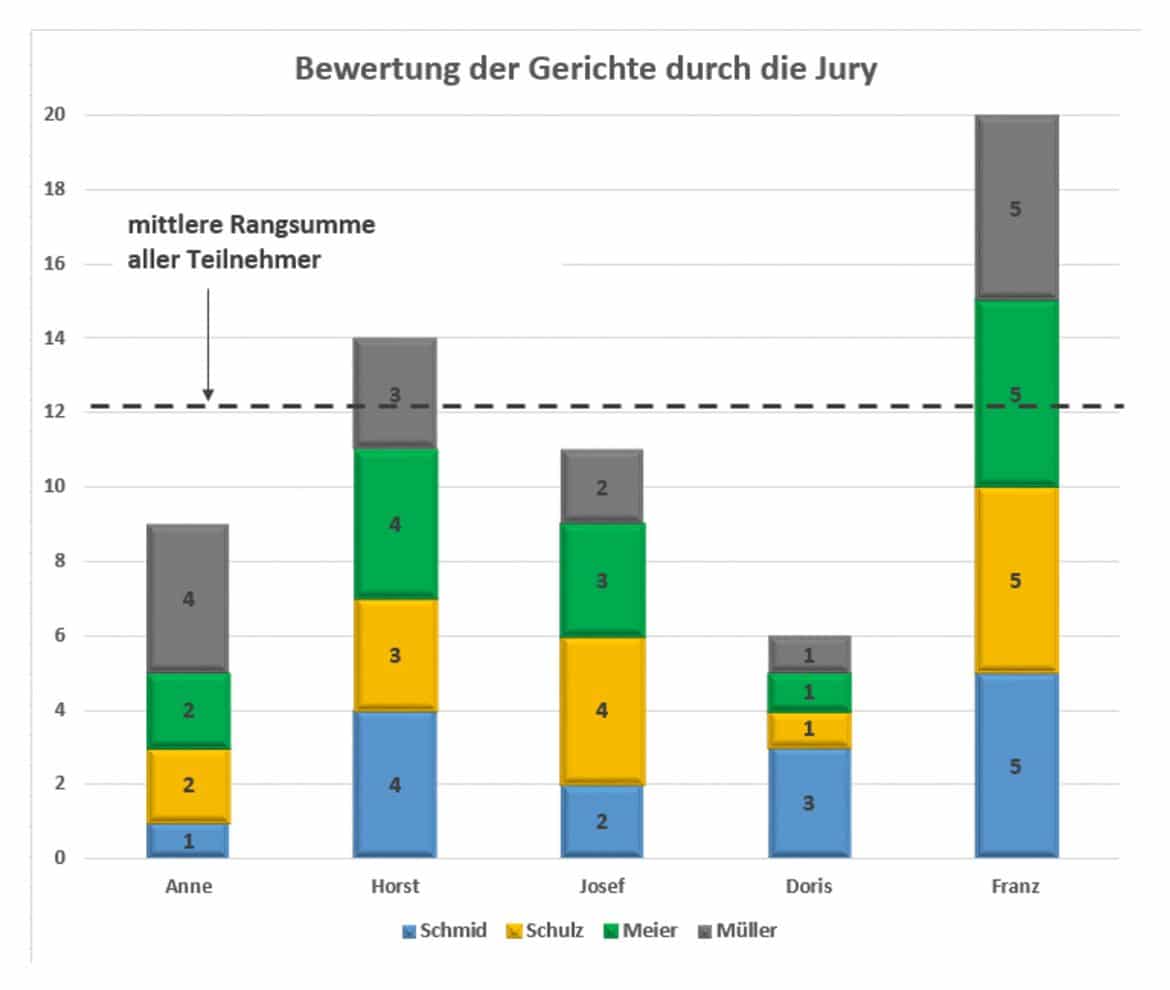
Wie berechnet man die Prüfgröße?

Du berechnest nun zuerst für jedes Objekt die Differenz zwischen seiner individuellen und der mittleren Rangsumme und quadrierst sie. Summierst Du diese Werte über alle Objekte und normierst, so ergibt sich Kendalls W der Konkordanzanalyse:

   

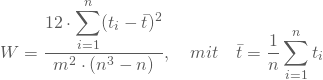
Sind Bindungen vorhanden, d. h. ordnen nicht alle Beurteiler jedem Objekt einen eindeutigen Rang zu, erfährt der Nenner eine Modifikation.

Kendalls W für Deinen Datensatz berechnest Du also zu:

   

Dieser Koeffizient zeigt folglich an, dass eine Übereinstimmung zwischen den Jurymitgliedern besteht. Er ist aber größenmäßig nicht mit den üblichen Korrelationskoeffizienten vergleichbar und entsprechend nicht analog interpretierbar.

Für oder ist das Produkt annähernd verteilt, mit Freiheitsgraden.

Um also die Hypothesen zu testen:

: Es besteht kein signifikanter Zusammenhang zwischen den Wertungen der Jurymitglieder und

: Es besteht ein signifikanter Zusammenhang zwischen den Wertungen der Jurymitglieder,

vergleichst Du mit bei (n-1) Freiheitsgraden zum Niveau von :

Für Dein Beispiel heißt das:

   

Du verwirfst damit die Nullhypothese und schließt, dass die abgegebenen Rangfolgen signifikant miteinander in Zusammenhang stehen.