Kolmogorov-Smirnov-Test / Liliefors-Test

Kolmogorov-Smirnov-Test / Liliefors-Test

  • 18. November 2016
  • Posted by: Mika
Keine Kommentare

Der Kolmogorov-Smirnov-Test ist ein Test, mit dem Du Deine Stichprobenergebnisse auf Übereinstimmung mit einer vermuteten Verteilung testen kannst. Er ist auch für kleinere Stichproben geeignet und kann auf alle Skalenniveaus angewendet werden.

Idee des Tests ist wie beim Chi-Quadrat-Anpassungstest, die beobachteten Häufigkeiten Deiner Stichprobe mit den theoretischen Häufigkeiten zu vergleichen, die zu erwarten wären, falls Deine Verteilungsvermutung zutrifft. Während beim Chi-Quadrat-Test alle Abweichungen in die Teststatistik einfließen, ist es hier nur der betragsmäßig höchste Wert.

Beim routinemäßigen CheckUp der Mitarbeiter einer Abteilung hast Du beispielsweise unter anderem das Körpergewicht ermittelt, in Gewichtsklassen j = 1 bis 7 eingeteilt und die Häufigkeiten n_j jeder Klasse bestimmt. Die ersten fünf Spalten der Tabelle zeigen dann das Ergebnis Deiner Untersuchung:

lfd. Nr. untere Grenze obere Grenze Klassenmitte beobachtete Häufigkeit relative Häufigkeit empirische Verteilung standardisierte Klassenmitte theoretische Verteilungsfunktion absolute Differenz
j x_j^u x_j^o x_j^m n_j h_j=\frac{n_j}{n} F_{emp}(j) z_j=\frac{x_j^m-\bar x}{s_x} F_{theor}=F_{NV}(z_j) F_{emp}-F_{theor}
1 50 60 55 2 0,05 0,05 -1,81 0,04 0,01
2 60 70 65 5 0,12 0,16 -1,22 0,11 0,05
3 70 80 75 10 0,23 0,40 -0,64 0,26 0,13
4 80 90 85 12 0,28 0,67 -0,05 0,48 0,20
5 90 100 95 4 0,09 0,77 0,53 0,70 0,06
6 100 110 105 5 0,12 0,88 1,12 0,87 0,02
7 110 124 117 5 0,12 1,00 1,82 0,97 0,03
insgesamt 43 1,00

Die relativen Häufigkeiten erhältst Du aus den beobachteten Häufigkeiten, dividiert durch die Gesamtzahl der Beobachtungen:

    \begin{equation*} h_j = \frac {n_j}{n}; \end{equation*}

die empirische Verteilungsfunktion durch Kumulieren der relativen Häufigkeiten zu:

    \begin{equation*} F_{emp}(j)=\sum_{i=1}^j h_j = \sum_{i=1}^j \frac {n_i}{n} \end{equation*}

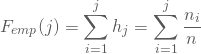
Für Deine weitere Analyse der Daten wäre es gut, wenn Du für die Zufallsvariable „Körpergewicht“ Normalverteilung unterstellen könntest. Daher formulierst Du folgende Hypothesen:

Aufstellen von Hypothesen

H_0: die Zufallsvariable „Körpergewicht“ ist normalverteilt.

H_1: die Zufallsvariable „Körpergewicht“ ist nicht normalverteilt.

Um die theoretischen Wahrscheinlichkeiten bei Zutreffen der Normalverteilung zu ermitteln, standardisierst Du zuerst die Klassenmitten mit den Schätzwerten für Mittelwert und Standardabweichung aus Deiner Stichprobe

    \begin{equation*} \bar x = 85,9 \quad und \quad s_x = 17,1 \end{equation*}

zu

    \begin{equation*} z_j = \frac {x_j^m - \bar x}{s_x}. \end{equation*}

Zu diesen z_j ermittelst Du dann die Werte der theoretischen Verteilungsfunktion F_{theor}=F_{NV}(z_j) als Wahrscheinlichkeit, mit der bei Gelten der Nullhypothese ein standardisierter Wert kleiner oder gleich z_j beobachtet würde.

Abweichungen zwischen beobachteter und erwarteter Wahrscheinlichkeit

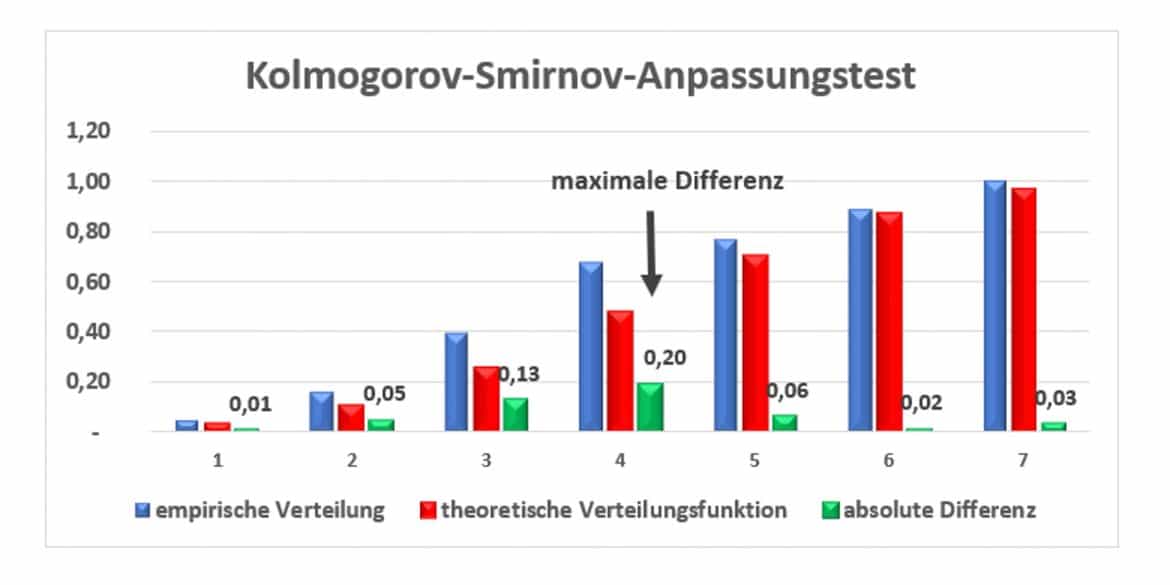
Dann berechnest Du für jedes j die absolute Differenz zwischen der empirischen und theoretischen Verteilungsfunktion, wie in der letzten Tabellenspalte erfolgt. Der größte dieser Werte ist Deine Prüfgröße, hier ist d_{pr}=0,20 für j=4.

In der Grafik siehst Du die empirische und theoretische Verteilungsfunktion sowie in grün die absolute Differenz zwischen beiden. Letztere nimmt ihren größten Wert mit d_{pr}=0,20 für j=4 ein.

 

Die kritischen Werte liegen für kleine Stichprobenumfänge tabelliert vor und lassen sich ab n=35 durch Näherungsformeln errechnen, für \alpha = 5\% gilt: d_{kr}= \frac {1,358} {\sqrt{n} }

Mit

    \begin{equation*} 0,20 = d_{pr} < d_{kr} = 0,2071 \end{equation*}

kannst Du die Nullhypothese nicht verwerfen und schließt, dass die Stichprobenwerte die vermutete Normalverteilung nicht widerlegen.

Der Kolmogorov-Smirnov-Test ist einerseits ein robuster Test für alle Skalenniveaus. Für quantitative Merkmale ist er jedoch andererseits wenig trennscharf. Diese Überlegung greift der Lilliefors-Test auf und passt den Kolmogorov-Smirnov-Test für den speziellen Fall einer Normalverteilung an, ist aber in seiner Teststärke sowohl dem Anderson-Darling-Test als auch dem Shapiro-Wilk-Test unterlegen.