Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Cramér-von-Mises-Test
- 26. April 2018
- Posted by: Mika
Mit dem Cramér-von Mises-Test vergleichst Du zwei Verteilungen und prüfst die Hypothese, dass beide gleich sind. Als Prüfgröße ![]() berechnest Du dazu das Integral der quadratischen Abweichungen beider Verteilungen:
berechnest Du dazu das Integral der quadratischen Abweichungen beider Verteilungen:
![]()
Du kannst den Test auf zwei verschiedene Situationen anwenden:
- Im Ein-Stichproben-Fall testest Du, ob die empirische Verteilung Deiner Stichprobe mit der Annahme einer theoretischen Verteilung vereinbar ist. Dann ist
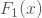 die empirische Verteilung Deiner Stichprobe und
die empirische Verteilung Deiner Stichprobe und 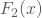 die angenommene theoretische Verteilung.
die angenommene theoretische Verteilung. - Im Zwei-Stichproben-Fall vergleichst Du die beiden empirischen Verteilungen Deiner Stichproben.
Ein-Stichproben-Fall:
Stell Dir vor, Du erhebst in einer Stichprobe das Alter der Studienanfänger an Deiner Uni und möchtest testen, ob Deine Annahme einer Normalverteilung mit den Daten vereinbar ist. Du erhältst die folgenden Altersangaben, der Größe nach geordnet:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 16 | 17 | 17 | 18 | 18 | 18 | 19 | 19 | 19 | 20 | 20 | 24 | |
| -1,341 | -0,853 | -0,853 | -0,366 | -0,366 | -0,366 | 0,122 | 0,122 | 0,122 | 0,610 | 0,610 | 2,560 | |
| 0,090 | 0,197 | 0,197 | 0,357 | 0,357 | 0,357 | 0,549 | 0,549 | 0,549 | 0,729 | 0,729 | 0,995 |
Du standardisierst nun Deine ![]() , indem Du ihren Mittelwert
, indem Du ihren Mittelwert ![]() von ihnen subtrahierst und die Differenz durch die Standardabweichung dividierst; anschließend ermittelst Du die Werte der Standardnormalverteilung an den Stellen
von ihnen subtrahierst und die Differenz durch die Standardabweichung dividierst; anschließend ermittelst Du die Werte der Standardnormalverteilung an den Stellen ![]() .
.
Dann berechnest Du den Wert der Testgröße
![Rendered by QuickLaTeX.com \begin{equation*} T=\omega^2_n = \frac {1} {12 n}+ \sum_{i=1}^n \left[ \frac {2i - 1}{2n} - F(x_i)\right]^2 \end{equation*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-7b76b052489e1ace9952a251ebeb3506_l3.png)
Für Dein Beispiel erhältst Du T=0,065.
Diesen Prüfwert vergleichst Du mit dem kritischen Wert aus der testspezifischen Tabelle und verwirfst die Nullhypothese, wenn der Prüfwert größer als der kritische Wert zum Niveau ![]() ist.
ist.
Mit ![]() verwirfst Du die Nullhypothese bei einer Irrtumswahrscheinlichkeit von
verwirfst Du die Nullhypothese bei einer Irrtumswahrscheinlichkeit von ![]() nicht.
nicht.
Zwei-Stichproben-Fall:
Für den Zwei-Stichproben-Fall unterstellt der Test, dass keine Bindungen, also das Auftreten von gleichen Werten, auftreten. Erhebst Du etwa das Alter der weiblichen und männlichen Studienanfänger getrennt voneinander, so kannst Du mit diesem Test die Verteilung der beiden Stichproben vergleichen.
Du hast etwa bei einer Erhebung vermerkt, ob es sich um einen Studentin (w) oder einen Studenten (m) handelt. Deine Stichprobe besteht beispielsweise aus n=4 Studentinnen und m=3 Studenten, deren Alter in eine gemeinsame Rangordnung gebracht wurde:
| i | gemeinsame Rangordnung | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 16 | 17 | 18 | 19 | 20 | 21 | 24 | ||
| Geschlecht | w | w | m | m | w | m | w | |
| Rangordnung Studentinnen |
1 | 2 | 3 | 4 | ||||
| Rangordnung Studenten | 1 | 2 | 3 |
Daraus berechnest Du als Prüfgröße
![]()
mit
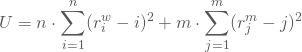
![]() stellt den Rangwert der i-ten Studentin innerhalb der weiblichen Stichprobe,
stellt den Rangwert der i-ten Studentin innerhalb der weiblichen Stichprobe, ![]() den des j-ten Studenten innerhalb der männlichen Stichprobe dar.
den des j-ten Studenten innerhalb der männlichen Stichprobe dar.
Für Dein Beispiel erhältst Du
![]()
und damit
![]()
Vergleichst Du den Wert der Prüfgröße mit dem kritischen Wert aus der Tabelle des Cramér-von-Mises-Test zum Niveau von $\alpha=0,05 und n=4, so kannst Du mit
![]()
die Nullhypothese, die Verteilungen seien gleich, nicht verwerfen.
