Binomialtest

Binomialtest

  • 31. Mai 2017
  • Posted by: Mika
Keine Kommentare

Der Binomialtest überprüft, ob die Häufigkeitsverteilung einer dichotomen Variable zufällig entstanden ist oder nicht. Damit kannst Du Aussagen über die Wahrscheinlichkeit treffen, mit der eine der beiden Ausprägungen auftritt. Die Teststatistik des Binomialtests beruht (wie der Name schon sagt) auf der Binomialverteilung.

Stell Dir vor, Du führst in einem Unternehmen eine Untersuchung zum Ess- und Trinkverhalten des Personals durch. Dabei bringst Du in Erfahrung, dass nach der Mittagspause eher Kaffee (75 %) statt Tee (25 %) getrunken wurde. Du untersuchst also die Variable „Getränk“ mit den dichotomen Ausprägungen „Kaffee“ und „Tee“. Nun fragst Du Dich, ob Deine Entdeckung zufällig entstanden ist oder ob Du einen Effekt gefunden hast, den Du gerne genauer analysieren würdest.

Binomialtest zum Überprüfen einer Hypothese

Um eine Hypothese mittels Binomialtest beantworten zu können benötigst Du immer eine Wahrscheinlichkeit, mit der Du das von Dir entdeckte Ergebnis vergleichen kannst. Bezogen auf unser Beispiel bräuchtest Du also eine theoretische Wahrscheinlichkeit hinsichtlich des Anteils an Tee bzw. Kaffee trinkenden Menschen. Diese dient dann als Referenz für Deine Entdeckung. Nehmen wir an, dass Du Dir diese theoretische Wahrscheinlichkeit aus einer Studie ableitest, die sich genau mit diesem Thema auseinandergesetzt hat und eine große Stichprobe umfasst. Die Studie kam zu dem Resultat, dass 50 % ihrer Teilnehmer Tee und 50 % Kaffee konsumieren.

Die Grundannahme des Binomialtests bzw. die Nullhypothese ist, dass Dein Ergebnis zufällig zustande gekommen ist (= Zufallsvariable) und sich nicht von der theoretischen Wahrscheinlichkeit unterscheidet. Getestet wird somit, ob die von Dir beobachtete Häufigkeit einer der Ausprägungen (in diesem Fall Tee oder Kaffee) mit der postulierten Wahrscheinlichkeit übereinstimmt.

Es ist nicht notwendig beide Ausprägungen der dichotomen Variable zu testen, da sich die Wahrscheinlichkeit des Auftretens der einen Ausprägung aus der anderen ergibt (75 % Kaffee ergeben automatisch 25 % Tee, wenn es nur zwei Ausprägungen gibt). Du kannst deine Hypothese also entweder auf Tee oder Kaffee beschränken.

Einseitig oder zweiseitig testen

Nun bleibt noch zu überlegen, ob Du Deine Hypothese einseitig oder zweiseitig formulierst. Eine zweiseitige Formulierung bedeutet, dass sich die theoretische und die beobachtetet Häufigkeitsverteilung Deiner Meinung nach unterscheiden. Dabei machst Du aber keine Aussagen darüber, ob Deine Stichprobe bspw. mehr oder weniger Kaffee konsumiert, als die Referenz, sondern gehst nur davon aus, dass ein Unterschied besteht.

Wenn Du aber bestimmte Erwartungen hast, in welche Richtung dieser Unterschied geht (also bspw. mehr Kaffeekonsum als aus der Theorie zu erwarten wäre), kannst Du eine einseitige Testung durchführen. Bei einer einseitig formulierten Hypothese hat der Binomialtest größere Testmacht, als bei einer zweiseitig formulierten. Allerdings kann es sein, dass Du signifikante Effekte übersiehst, wenn Du nur einseitig testest, da Du nicht beide Seiten der Verteilung statistisch überprüfst.

Sehen wir uns die zweiseitige Testung anhand des Beispiels an. Angenommen von 20 nach der Mittagspause konsumierten Getränken waren 15 Kaffee (= 75 %) und 5 Tee (= 25%). Die Frage ist nun, ob sich Deine beobachtete Häufigkeit signifikant von der theoretischen Häufigkeit unterscheidet.

Aufstellen von Hypothesen

Die Hypothesen lassen sich in H_{0} und H_{1} ausgedrückt auch folgendermaßen darstellen:

    \begin{equation*} \begin{split} \ H_{0}: \text{Auftretenswahrscheinlichkeit beobachtete Haeufigkeit =} \\ \text{Auftretenswahrscheinlichtkeit theoretische Haeufigkeit} \end{split} \end{equation*}

    \begin{equation*} \begin{split} \ H_{1}: \text{Auftretenswahrscheinlichkeit beobachtete Haeufigkeit} \neq \\ \text{Auftretenswahrscheinlichtkeit theoretische Haeufigkeit} \end{split} \end{equation*}

 

oder knapper ausgedrückt:

    \begin{equation*} \ H_{0}: p=p_{0} \end{equation*}

    \begin{equation*} H_{1}: p\neq p_{0} \end{equation*}

Wenn Du Dich im Rahmen des Beispiels auf Kaffee als Zielvariable fokussierst, ergeben sich damit folgende Hypothesen:

    \begin{equation*} \ H_{0}: p=0.50 \end{equation*}

    \begin{equation*} H_{1}: p\neq 0.50 \end{equation*}

Der Wert 0.50 resultiert aus der theoretischen Recherche, könnte aber auch bspw. 0.25 betragen, wenn die Referenzstudie gezeigt hätte, dass 25 % ihrer Teilnehmer Kaffee statt wählten.

Nun bleibt noch ein Signifikanzniveau zu wählen (bspw. \alpha=.05) und zu überprüfen, ob sich die beobachteten und theoretischen Häufigkeiten signifikant unterscheiden. Dazu kannst Du entweder Statistiksoftware verwenden oder in einer Tabelle nachschlagen, die Werte bezüglich Binomialverteilung enthält.

Eine Analyse mit entsprechender Statistiksoftware zeigt Dir, dass sich Deine beobachtete Häufigkeit signifikant von der theoretischen Häufigkeit unterscheidet \left(\mathbold{p}=.041\right). D. h. Du kannst die Nullhypothese verwerfen, da die Verteilung nicht zufällig entstandenen ist und mit Hilfe weiterer Beobachtungen versuchen der Ursache auf den Grund zu gehen, wieso in diesem Unternehmen nach der Mittagspause häufiger Kaffee als Tee konsumiert wird.

Binomialtest per Hand

Nun versuchen wir dieses Ergebnis mit der tabellarischen Methode zu replizieren. Um die richtigen Werte aus der Tabelle abzulesen, ist es wichtig folgende Informationen zu berücksichtigen:

  • Stichprobengröße (n = 20 bei unserem Beispiel)
  • Referenzwahrscheinlichkeit (in unserem Fall 0.5 bzw. 50%, da dies die Information der Referenzstudie ist)
  • Signifikanzniveau (hier \alpha=.05)

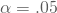Hast Du die passende Tabelle gefunden (Vorsicht – manche Tabellen geben bspw. Werte für n = 100 aus, achte also genau auf die Stichprobengröße) musst Du in der Spalte die p = 0.5 (und n = 20) anzeigt nach einem Zahlenwert suchen, der möglichst nahe an 0.025 liegt, diesen Wert aber nicht übersteigt. Die Zahl 0.025 spiegelt das halbierte Signifikanzniveau wider. Hast in der Tabelle den nächsten an 0.025 liegenden Wert gefunden, der 0.025 aber noch nicht übersteigt (du solltest auf diese 0.0148 ermittelt haben), kannst aus der Tabelle ablesen, wie klein oder groß der zugehörige Wert „k“ ist.

Mit Hilfe von „k“ wird die Anzahl an Beobachtungseinheiten einer bestimmten Ausprägung beschrieben. Bei unseren beobachteten Daten ist bspw. k = 15, da sich 15 Personen für Kaffee entschieden haben. Der tabellarische Wert 0.0148 führt zu den k-Werten 5 und 15. Das bedeutet, mindestens 15 oder maximal 5 Personen müssen sich für Kaffee entschieden haben, damit sich unsere beobachteten Daten bei einer Stichprobengröße von n = 20 und einem Signifikanzniveau \alpha=.05 signifikant von dem Referenzdatensatz unterscheiden. Hätten nur 14 Personen Kaffee gewählt, wäre das tabellarische \alpha=.0370 und damit zahlenmäßig größer als 0.025 (damit wäre das Ergebnis nicht signifikant). Wichtig ist zu beachten, dass Du beim zweiseitigen testen den \alpha-Wert halbieren musst (deshalb 0.025 statt 0.05).

Insgesamt können wir also sowohl mittels Software als auch mit Hilfe der Tabelle die Nullhypothese verwerfen und kommen zu derselben Schlussfolgerung.