Anderson-Darling-Test

Anderson-Darling-Test

  • 18. November 2016
  • Posted by: Mika
Keine Kommentare

Du hast eine Stichprobe für eine metrisch skalierte Zufallsvariable erhoben. Nun möchtest Du prüfen, ob die Daten der Stichprobe Deine Vermutung einer bestimmten Verteilung der Zufallsvariablen in der Grundgesamtheit zulassen. Dafür hast Du mit dem Anderson-Darling-Test einen starken Test gegeben. Denn dieser kann auf verschiedene Verteilungen testen. Vor allem an den Rändern ist er stärker als der \chi^2- und der Kolmogorov-Smirnov-Anpassungstest.

Stell Dir vor, Du untersuchst Patienten mit einer seltenen Herzkrankheit und hast für 11 Patienten eine Reihe von Werten erhoben. Dazu zählt beispielsweise der systolische Blutdruck. Für die weitere Analyse wäre es gut, wenn Du Normalverteilung unterstellen könntest. Denn Du möchtest möglichst aussagekräftig testen, ob der systolische Blutdruck bei dieser Patientengruppe erhöht ist.

Testen auf Normalverteilung

Du entscheidest Dich daher für einen vorgelagerten Test, der diese Verteilungsvermutung unterstützen oder verwerfen soll. Dafür wählst Du hier den Anderson-Darling-Test aus. Deine Hypothesen lauten:

H_0: die Zufallsvariable „Systolischer Blutdruck“ folgt einer Normalverteilung

H_1: die Zufallsvariable „Systolischer Blutdruck“ folgt keiner Normalverteilung

Für den Test ordnest Du zunächst die Stichprobenwerte der Größe nach an und ermittelst den Mittelwert und die Standardabweichung aus der Stichprobe. Die z_i in der dritten Spalte der Tabelle erhältst Du als Differenz zwischen beobachtetem Wert und Mittelwert, dividiert durch die Standardabweichung.

Werte gemäß Verteilungsannahme

Für jedes der z_i bestimmst Du den Wert der Standardnormalverteilung an dieser Stelle (Spalte 4) sowie ihr Komplement (Spalte 5). Damit hast Du für den Fall, dass die Normalverteilung gilt, für jeden aufgetretenen Stichprobenwert die Wahrscheinlichkeiten berechnet, dass ein kleinerer bzw. ein größerer Wert als der realisierte auftritt.

Lfd. Nummer
i		 Systolischer 
Blutdruck
x_i		 Standardisierter Wert
z_i		 Verteilung 
der NV(z_i)
 Komplement der NV: 
1- F_{NV}(z_i)
1 54 – 1,871 0,0306 0,9694
2 73 – 0,760 0,2236 0,7764
3 76 – 0,585 0,2793 0,7207
4 76 – 0,585 0,2793 0,7207
5 79 – 0,409 0,3411 0,6589
6 83 – 0,175 0,4304 0,5696
7 94 0,468 0,6801 0,3199
8 94 0,468 0,6801 0,3199
9 97 0,643 0,7400 0,2600
10 104 1,053 0,8537 0,1463
11 116 1,754 0,9603 0,0397

Falls die Vermutung der Normalverteilung zutreffend ist, sind die auftretenden Werte symmetrisch um den Mittelwert angeordnet, und die Wahrscheinlichkeit, dass ein kleinerer Wert als (-z) auftaucht ist genauso groß wie die Wahrscheinlichkeit, dass ein Wert größer als z beobachtet wird. Auf dieser Überlegung basiert der Anderson-Darling-Test.

Prüfung auf Symmetrie

Du bildest Paare von Stichprobenwerten aus je zwei gegenüberliegenden Beobachtungswerten, dem kleinsten und dem größten Beobachtungswert, im Beispiel Beobachtungsnummern 1 und 11, dann aus dem zweitkleinsten und dem zweitgrößten Beobachtungswert, das sind hier Beobachtungsnummern 2 und 10, usw. bis hin zum Paar aus der größten und der kleinsten Beobachtung, also Beobachtungswerte 11 und 1.

Bei allen Paaren vergleichst Du die unter der Nullhypothese geltenden Wahrscheinlichkeiten für das Auftreten eines extremeren Wertes als dem beobachteten.

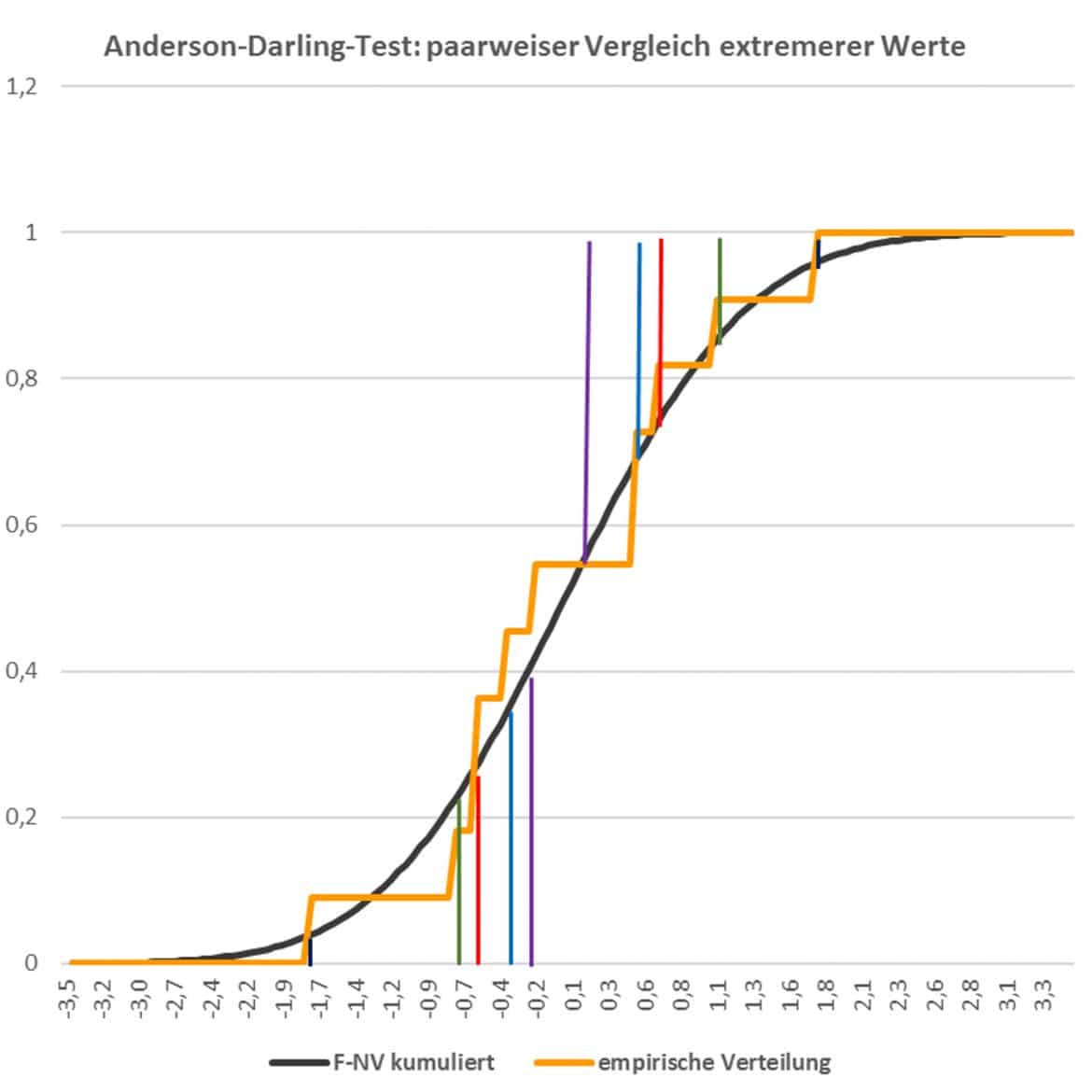
Empirische Verteilungsfunktion

Die Grafik zeigt die empirische Verteilungsfunktion Deines Beispiels in gelb sowie die Verteilungsfunktion der Standardnormalverteilung in schwarz eingezeichnet an. Überall dort, wo die empirische Verteilungsfunktion eine Sprungstelle aufweist, liegt ein standardisierter Stichprobenwert auf der x-Achse vor. An diesen Sprungstellen der gelben empirischen Veteilung findest Du für die ersten fünf Paare die Wahrscheinlichkeiten eingezeichnet, dass im Fall einer Normalverteilung ein extremerer Wert als der beobachtete auftaucht.

Für das Paar (1,11) beispielsweise, in schwarz eingezeichnet, erkennst Du an der Stelle z_1 = -1,871 die Wahrscheinlichkeit, mit der im Fall einer Standardnormalverteilung ein kleinerer Wert beobachtet würde, sowie an der Stelle z_{11} = 1,754 die Wahrscheinlichkeit, mit der bei Geltung der Standardnormalverteilung ein größerer Wert auftreten würde.

anderson-darling-test

Teststatistik des Anderson-Darling-Tests

Die Teststatistik ist gegeben durch

    \begin{equation*} A^2=-n-S, mit \quad S = \displaystyle \sum_{i=1} ^n \frac {2i-1}{n }\cdot [ln(F_{NV}(x_i) + ln(1-F_{NV}(x_{n+1-i}))] \end{equation*}

und logarithmiert diese Wahrscheinlichkeiten für das Auftreten von extremeren Werten und subtrahiert sie dann paarweise von außen nach innen voneinander. Damit ist sie ein Maß für die Abweichung der zu überprüfenden Theorie von der Realität. Stephens hat ein Verfahren dazu entwickelt, das für diesen Test eine direkte Abschätzung des p-Wertes aus der Testgröße ermöglicht.

Statistikprogrammsysteme geben neben der Teststatistik diesen zugehörigen p-Wert aus. Ist er größer als das gewünschte Signifikanzniveau \alpha, so gibt es aufgrund der Stichprobe keinen Anlass, die Nullhypothese zu verwerfen; ist der p-Wert kleiner als \alpha, so wird die Nullhypothese verworfen und die angenommene Verteilung hat sich als falsch erwiesen.

Für Dein Beispiel, das auch grafisch deutliche Abweichungen der beiden Verteilungen zeigt, testest Du zum Niveau \alpha= 0,05. Mit dem p-Wert von 0,00001 < 0,05 wird die Nullhypothese verworfen und Du kannst für das weitere Vorgehen mit Deinen Daten keine Normalverteilung annehmen.