Exakter Fisher-Test

Exakter Fisher-Test

  • 26. April 2018
  • Posted by: Mika
Keine Kommentare

Mit dem exakten Fisher-Test kannst Du prüfen, ob zwei dichotome Merkmale X und Y unabhängig voneinander sind. Damit stellt er eine Alternative zum Chi-Quadrat-Unabhängigkeitstest dar, die ohne Voraussetzungen an die Stichprobengröße auskommt und robuste Ergebnisse liefert.

Ausgangspunkt ist eine 4-Felder Kontingenztafel, in die Du die beobachteten Häufigkeiten n_{ij} einträgst, mit denen die i-te Ausprägung des Merkmals X zusammen mit der j-ten Ausprägung des Merkmals Y beobachtet wurde.

Du möchtest etwa untersuchen, ob der Wunsch, als Student in eine WG oder in ein Einzelzimmer zu ziehen, sich bei weiblichen und männlichen Studenten unterscheidet. Dazu befragst Du 20 Studenten. Die Tabelle zeigt die Ergebnisse der Befragung:

Y: Geschlecht
Y_1: weiblich Y_2:männlich
X: Wohnungs-
wunsch		 X_1: WG n_{11}=3 n_{12}=7 n_{1 \cdot}=10
X_2: EZ n_{21}=5 n_{22}=5 n_{2 \cdot}=10
n_{ \cdot 1}=8 n_{ \cdot 2}=12 n = 20

Du möchtest testen, ob die beobachteten Werte zum gewählten Signifikanzniveau mit der Nullhypothese vereinbar sind, dass Unabhängigkeit zwischen X und Y besteht:

H_0: X und Y sind unabhängig voneinander

gegen

H_1: X und Y sind abhängig voneinander.

Der Fisher-Test geht dazu von folgender Überlegung aus: Sind die Randhäufigkeiten n_{i \cdot} und n_{\cdot j} und der Inhalt eines der vier Felder bekannt, so sind dadurch die anderen drei Häufigkeiten ebenfalls eindeutig bestimmt: Mit n_{1 \cdot}=10 und n_{11}=3 beispielsweise muss n_{12}=7 sein, usw..

Für die Konstruktion des Tests reicht es daher aus, die Verteilung des linken oberen Feldes Deiner Kontingenztabelle zu betrachten. Fisher zeigte, dass die im linken oberen Feld erwartete Häufigkeit hypergeometrisch verteilt ist, mit

    \begin{equation*} P(n_{11}=k) = \frac {\left(\begin {array} {11} n_{1 \cdot} \\k\end{array}\right) \cdot \left(\begin {array} {11} n_{2 \cdot } \\n_{\cdot 1}-k\end{array}\right)} {\left(\begin {array} {11} n \\n_{\cdot 1}\end{array}\right) }, \quad mit \nobreakspace 0 \le k \le min(n_{1 \cdot}, n_{\cdot 1}) \end{equation*}

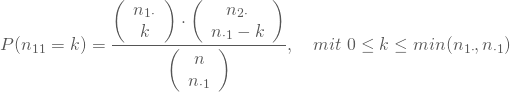
Für Dein Beispiel mit min(n_{1 \cdot}, n_{\cdot 1})=8 erhältst Du:

k P(n_{11}=k) F(k) =P(n_{11}\le k)
0 0,000 0,000
1 0,010 0,010
2 0,075 0,085
3 0,240 0,325
4 0,350 0,675
5 0,240 0,915
6 0,075 0,990
7 0,010 1,000
8 0,000 1,000

Dein gewähltes Signifikanzniveau \alpha bestimmt jetzt die Entscheidung Deines zweiseitigen Tests:

    \begin{equation*} H_0 \nobreakspace wird \nobreakspace verworfen, \nobreakspace falls \begin{cases} F(n_{11}) < \alpha/2, \nobreakspace f\"ur \nobreakspace n_{11} \le \frac k 2 \quad oder\\ \\ 1-F(n_{11})< \alpha/2, \nobreakspace f\"ur \nobreakspace n_{11} > \frac k 2. \end{cases} \end{equation*}

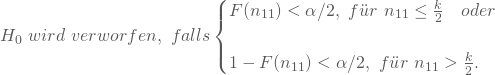
Tritt keiner der beiden Fälle ein, so sprechen Deine Werte nicht gegen die Nullhypothese.

Für \alpha = 0,05 und \frac {\alpha} 2 = 0,025 wird die Nullhypothese Deines Beispiels also nur verworfen, wenn Du im oberen linken Feld der Vierfeldertafel null oder eins bzw. sieben oder acht beobachtest hast.

Die Grafik zeigt die Testentscheidung des Beispiels:

Exakter Fisher-Test

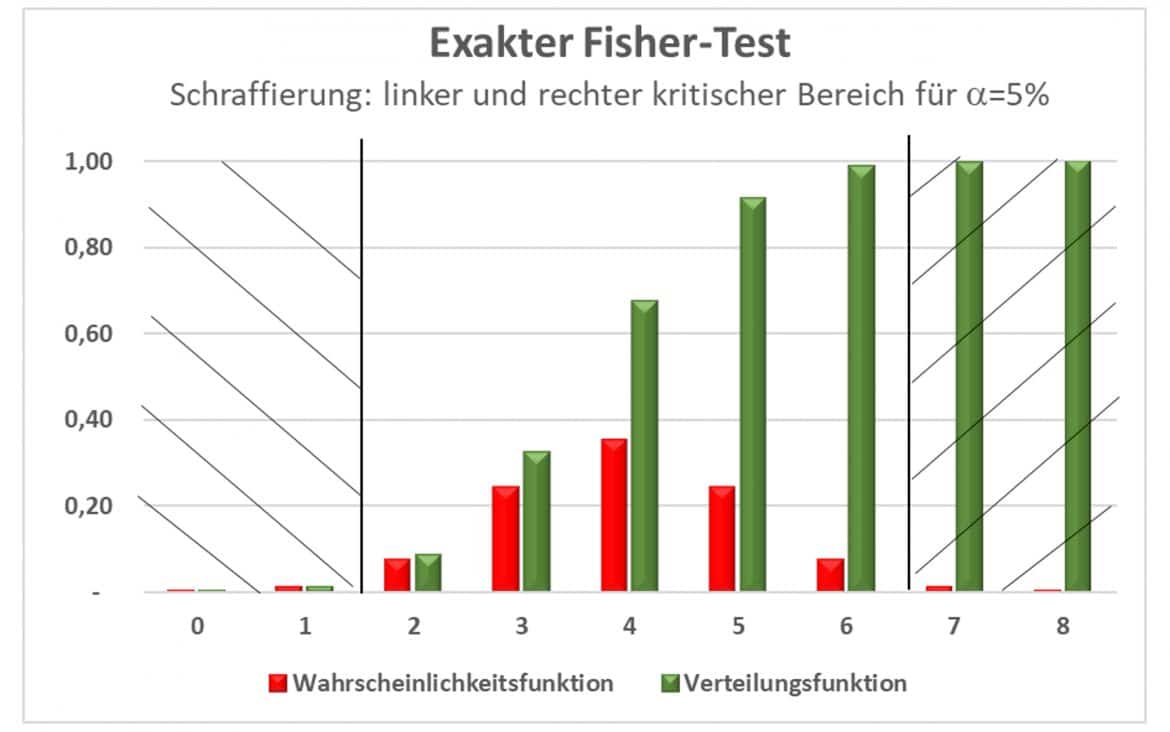
Die Wahrscheinlichkeit eines Fehlers zweiter Art, d.h. die Nullhypothese beizubehalten, obwohl sie falsch ist, ist dabei recht groß. Als Güte eines statistischen Tests bezeichnest Du die Wahrscheinlichkeit, keinen Fehler zweiter Art zu begehen. Damit kannst Du den exakten Fisher-Test beurteilen: Er ist zwar exakt, besitzt aber keine große Güte.

Falls die Voraussetzung für die Anwendung des Chi-Quadrat-Unabhängigkeitstests gegeben ist, falls also alle unter Unabhängigkeit zu erwartenden Häufigkeiten größer als fünf sind, solltest du ihn daher dem exakten Fisher-Test vorziehen.