Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Levene-Test
- 26. April 2018
- Posted by: Mika
Der Levene-Test untersucht k Stichproben von unabhängigen, stetig- (am besten normal-) verteilten Zufallsvariablen ![]() , i=1,…,k, auf Gleichheit ihrer Varianzen. Die Umfänge der Stichproben dürfen unterschiedlich groß sein.
, i=1,…,k, auf Gleichheit ihrer Varianzen. Die Umfänge der Stichproben dürfen unterschiedlich groß sein.
Im Gegensatz zum Bartlett-Test reagiert der Levene-Test robust auf Abweichungen von der Normalverteilung.
Er prüft die Nullhypothese
![]()
gegen die Alternativhypothese
![]()
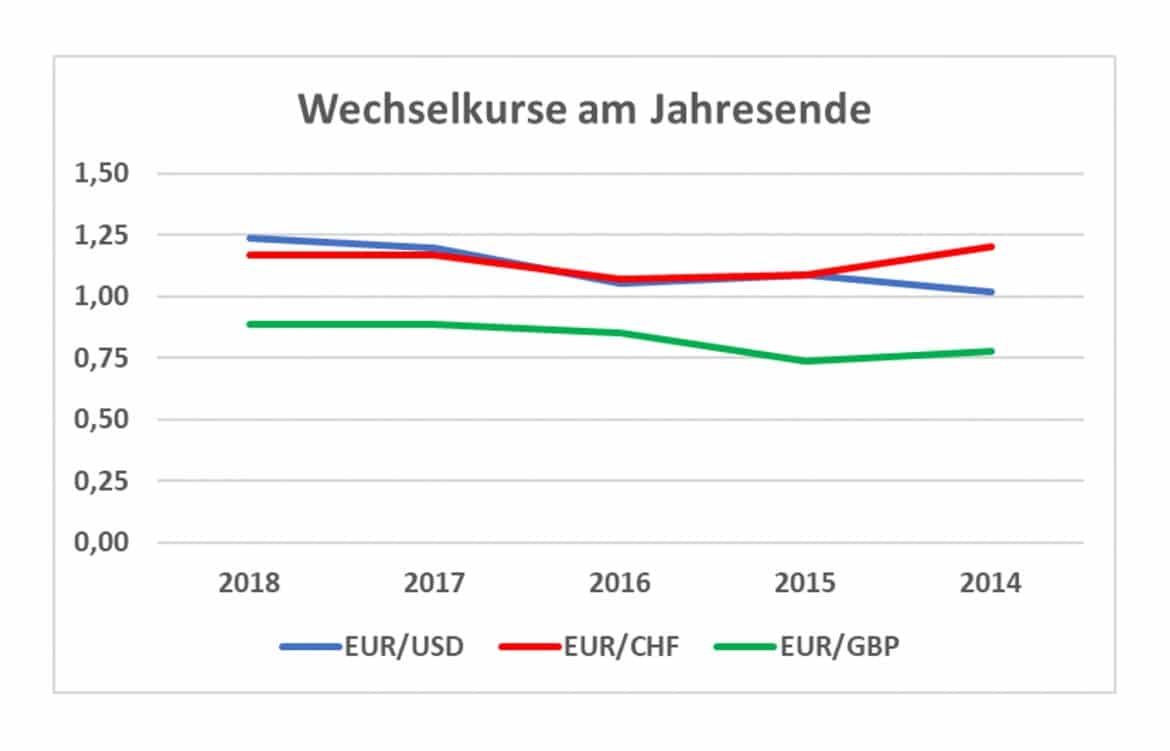
Stell Dir vor, Du betrachtest die jeweils am Jahresende notierten Wechselkurse dreier Währungen gegenüber dem Euro und möchtest prüfen, ob man gleiche Varianzen für alle drei unterstellen kann.
| Wechselkurse am Jahresende | |||
| EUR/USD |
EUR/CHF |
EUR/GBP |
|
| 2018 | 1,2366 | 1,1689 | 0,8857 |
| 2017 | 1,1994 | 1,169 | 0,8879 |
| 2016 | 1,0517 | 1,0711 | 0,8524 |
| 2015 | 1,086 | 1,0877 | 0,7364 |
| 2014 | 1,02098 | 1,2042 | 0,7764 |
| Mittelwert | 1,118936 | 1,14018 | 0,82776 |
Die Grafik visualisiert Dir den Verlauf der Wechselkurse:
Ansatzpunkt des Tests sind die absoluten Abweichungen ![]() der Stichprobenwerte
der Stichprobenwerte ![]() vom jeweiligen Stichprobenmittel
vom jeweiligen Stichprobenmittel ![]() :
:
![]()
Aus diesen absoluten Abweichungen berechnest Du die Stichprobenmittel ![]() und das Gesamtmittel
und das Gesamtmittel ![]()
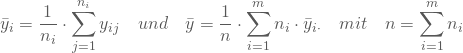
| Absolute Abweichung der Wechselkurse von ihrem Mittel | |||
| EUR/USD |
EUR/CHF |
EUR/GBP |
|
| 2018 | 0,117664 | 0,02872 | 0,05794 |
| 2017 | 0,080464 | 0,02882 | 0,06014 |
| 2016 | 0,067236 | 0,06908 | 0,02464 |
| 2015 | 0,032936 | 0,05248 | 0,09136 |
| 2014 | 0,097956 | 0,06402 | 0,05136 |
| Mittelwert |
0,0792512 | 0,048624 | 0,057088 |
| Gesamtmittelwert |
0,0616544 | ||
Damit bestimmst Du die gewichteten Varianzen zwischen (![]() ) und innerhalb (
) und innerhalb (![]() ) den absoluten Abweichungen der Stichproben.
) den absoluten Abweichungen der Stichproben.
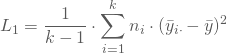
und
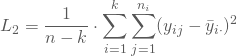
Deine Prüfgröße L erhältst Du als Quotienten aus ![]() und
und ![]() ; sie ist unter der Nullhypothese F-verteilt, mit ((k-1);(n-k)) Freiheitsgraden.
; sie ist unter der Nullhypothese F-verteilt, mit ((k-1);(n-k)) Freiheitsgraden.
Die Nullhypothese wird verworfen, wenn L größer als der kritische Wert der F-Verteilung zum gewählten Signifikanzniveau ist.
Für Dein Beispiel erhältst Du:
![]()
und
![]()
Damit lautet Deine Testentscheidung:
![]()
Die Nullhypothese der einheitlichen Varianz wird nicht verworfen, denn Deine Stichproben geben dazu nach dem Levene-Test keinen Anlass.
Falls Normalverteilung der Grundgesamtheiten gegeben ist, solltest Du Dich beim Test auf Varianzhomogenität des Bartlett-Tests bedienen, der unter dieser Voraussetzung trennschärfer ist. Liegt keine Normalverteilung vor, verhält sich der Levene-Test robuster und ist dann vorzuziehen.
