Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
F-Test
- 26. Januar 2017
- Posted by: Mika
Mit dem F-Test kannst Du zwei Stichproben aus normalverteilten Grundgesamtheiten mit den unbekannten Parametern ![]() und
und ![]() sowie
sowie ![]() und
und ![]() darauf untersuchen, ob signifikante Unterschiede bei den Varianzen bestehen.
darauf untersuchen, ob signifikante Unterschiede bei den Varianzen bestehen.
Stell Dir vor, Du möchtest in Aktien investieren. Du hast zuerst an der Börse recherchiert und schwankst nun zwischen der Investition in Aktien der Firmen Albert (A) und Bernhard (B). Ein Insider hat Dir diese als annähernd gleich erfolgreich empfohlen. Du willst natürlich in das Unternehmen investieren, dessen Aktien mit dem kleineren Risiko von Kursschwankungen verbunden sind. Du weißt, dass Aktienkurse einer Normalverteilung folgen, und beschließt, Stichproben mit den Kursen beider Aktien über elf Monate hinweg jeweils am Monatsanfang zu erheben. Die Grafik zeigt den Verlauf der Kurse im vergangenen Jahr.
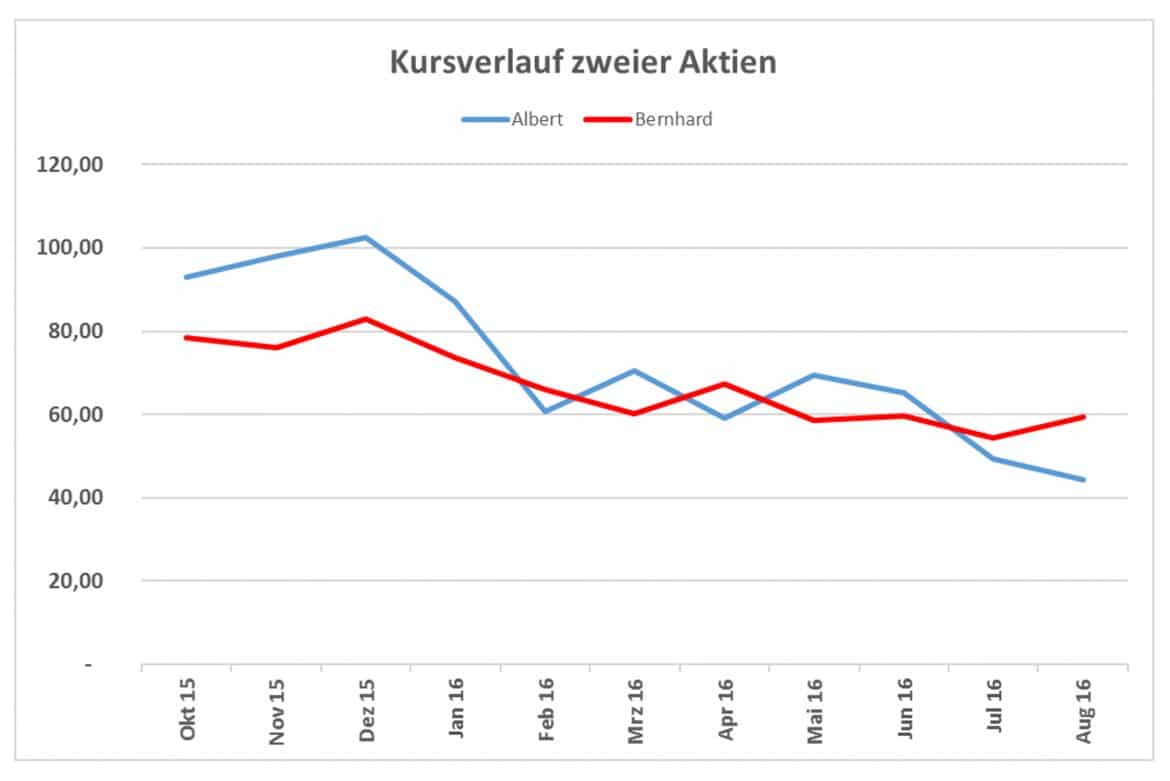
Für die beiden Stichproben ermittelst Du die Mittelwerte und Varianzen nach den Formeln:
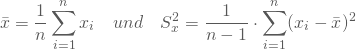
Die entsprechenden Werte findest Du in den letzten beiden Tabellenspalten.
| Aktie | Aug 16 | Jul 16 | Jun 16 | Mai 16 | Apr 16 | Mrz 16 | Feb 16 | Jan 16 | Dez 15 | Nov 15 | Okt 15 | Mittelwert | Stichproben- varianz |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| A | 44,32 | 49,28 | 65,12 | 69,44 | 59,20 | 70,56 | 60,60 | 87,16 | 102,60 | 97,96 | 93,00 | 72,66 | 390,85 |
| B | 59,35 | 54,24 | 59,61 | 58,68 | 67,28 | 60,28 | 65,93 | 73,63 | 82,84 | 76,01 | 78,55 | 66,95 | 90,10 |
Deine deutlich höhere Stichprobenvarianz bei den Kurswerten der Aktie A lässt vermuten, dass auch in den Grundgesamtheiten die Aktie A der Firma Albert eine höhere Varianz als B der Firma Bernhard aufweist.
Aufstellen von Hypothesen
Da Du immer nur den Fehler 1. Art kontrollieren kannst, formulierst Du Deine Hypothesen umgekehrt zu Deiner Vermutung:
![]()
Für die Teststatistik betrachtest Du dann den Quotienten der realisierten Stichprobenvarianzen
![]()
wobei ![]() die in der Nullhypothese als kleiner angenommene Stichprobenvarianz ist. Allgemein setzt Du im Fall einer ungerichteten Hypothese immer die größere Stichprobenvarianz in den Zähler, im Fall einer gerichteten Hypothese die, deren Varianz in der Nullhypothese als die kleinere vermutet wird.
die in der Nullhypothese als kleiner angenommene Stichprobenvarianz ist. Allgemein setzt Du im Fall einer ungerichteten Hypothese immer die größere Stichprobenvarianz in den Zähler, im Fall einer gerichteten Hypothese die, deren Varianz in der Nullhypothese als die kleinere vermutet wird.
Falls beide Varianzen gleich sind, beträgt ![]() . Du verwirfst die Nullhypothese also, falls die Prüfgröße „zu groß“ wird.
. Du verwirfst die Nullhypothese also, falls die Prüfgröße „zu groß“ wird.
Wie gelangt man zur Teststatistik?
Um Deine Entscheidung zu konkretisieren, musst Du wissen, welcher Verteilung ![]() folgt.
folgt.
Dazu betrachtest Du zunächst Zähler und Nenner der Prüfgröße genauer: Beide bestimmen sich als Summe von quadrierten, um ihren Mittelwert bereinigten normalverteilten Zufallsvariablen, jeweils dividiert durch die um eins reduzierte Stichprobengröße.
Teilst Du Zähler und Nenner durch die Varianz ![]() in der Grundgesamtheit (was den Wert des Quotienten nicht verändert) und multiplizierst mit dem Faktor
in der Grundgesamtheit (was den Wert des Quotienten nicht verändert) und multiplizierst mit dem Faktor ![]() , so folgen beide einer
, so folgen beide einer ![]() -Verteilung:
-Verteilung:
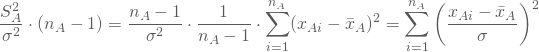
Der so erweiterte Zähler lässt sich als Summe von quadrierten Realisationen standardnormalverteilter Zufallsvariablen umformen: von jeder Beobachtung (der normalverteilten Zufallsvariablen) berechnest Du ihre Differenz zum Mittelwert, normierst diese durch Division durch die Standardabweichung und Du erhältst standardisierte Werte. Diese quadrierst Du dann und summierst über alle i.
Eine Summe quadrierter standardnormalverteilter Zufallsvariablen ist aber ![]() -verteilt, mit
-verteilt, mit ![]() Freiheitsgraden.
Freiheitsgraden.
Für den erweiterten Nenner gilt entsprechend:
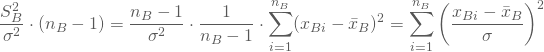
Er ist ![]() -verteilt, mit
-verteilt, mit ![]() Freiheitsgraden.
Freiheitsgraden.
Teilst Du jetzt beide ![]() verteilten Größen durch Ihre Freiheitsgrade und setzt sie als Zähler und Nenner ein, so erhältst Du eine F-verteilte Zufallsvariable und Deine obige Prüfgröße.
verteilten Größen durch Ihre Freiheitsgrade und setzt sie als Zähler und Nenner ein, so erhältst Du eine F-verteilte Zufallsvariable und Deine obige Prüfgröße.
![]() als Quotient zweier durch ihre Freiheitsgrade dividierter
als Quotient zweier durch ihre Freiheitsgrade dividierter ![]() -verteilter Zufallsvariablen folgt also einer F-Verteilung mit
-verteilter Zufallsvariablen folgt also einer F-Verteilung mit ![]() und
und ![]() Freiheitsgraden.
Freiheitsgraden.
Nach diesen Überlegungen kannst Du Deine Prüfgröße berechnen und sie mit dem Wert der F-Verteilung zum Niveau ![]() bei
bei ![]() Freiheitsgraden vergleichen.
Freiheitsgraden vergleichen.
Für Dein Beispiel ergibt sich:
![]()
Die Testentscheidung
Aufgrund Deiner Stichprobenergebnisse verwirfst Du die Nullhypothese und schließt mit einer Irrtumswahrscheinlichkeit von ![]() , dass die Varianz von B geringer ist als die von A.
, dass die Varianz von B geringer ist als die von A.
Damit ist Deine Kaufentscheidung gefallen: Dein Risiko bei der Anlage in Aktien B bei dem Unternehmen Bernhard ist signifikant geringer als bei der Investition in Aktien der Firma Albert.
In obigem Beispiel interessierte es Dich, die Varianzen als Maß für die Risiken Deiner in Frage kommenden Anlagevarianten zu vergleichen. Das Ergebnis des F-Tests war direkter Mittelpunkt Deines Interesses.
Oft verwendest Du den F-Test auch als vorgelagerten Test für andere statistische Verfahren, die Homoskedastizität, also Varianzgleichheit in der Grundgesamtheit voraussetzen. Varianzgleichheit lässt sich zwar nicht bestätigen, aber Du kannst immerhin prüfen, ob Deine Daten diese Vermutung zulassen oder sie widerlegen.
