Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Bartlett-Test
- 26. April 2018
- Posted by: Mika
Mit dem Bartlett-Test kannst Du k Stichproben von normalverteilten Zufallsvariablen
![]() , i=1,…,k, daraufhin untersuchen, ob sie die gleiche Varianz besitzen. Die Varianzanalyse beispielsweise benötigt diese Voraussetzung der Varianzhomogenität.
, i=1,…,k, daraufhin untersuchen, ob sie die gleiche Varianz besitzen. Die Varianzanalyse beispielsweise benötigt diese Voraussetzung der Varianzhomogenität.
Deine Hypothesen lauten:
![]()
gegen
![]()
Die Stichproben müssen nicht vom gleichen Umfang sein, aber Du benötigst mindestens 5 Beobachtungen für jede Stichprobe: ![]() für i = 1,…,k.
für i = 1,…,k.
Dann kannst Du aus jeder Stichprobe ![]() als Schätzwert für die Varianz der Grundgesamtheit aus der i-ten Stichprobe berechnen,
als Schätzwert für die Varianz der Grundgesamtheit aus der i-ten Stichprobe berechnen,
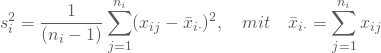
sowie ![]() als gewichtete Mittelwert der
als gewichtete Mittelwert der ![]() über alle Stichproben:
über alle Stichproben:
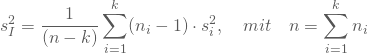
Bartlett entwickelte daraus eine Prüfgröße, die die logarithmierte durchschnittliche (gepoolte) Varianz mit der Summe der logarithmierten Varianzschätzungen der einzelnen Stichproben vergleicht; er zeigte, dass diese Prüfgröße ![]() -verteilt ist, mit
-verteilt ist, mit ![]() Freiheitsgraden.
Freiheitsgraden.
![Rendered by QuickLaTeX.com \begin{equation*} \chi^2_{pr}= \frac 1 C [(n-r) \cdot ln \nobreakspace s_I^2 - \sum_{i=1}^k (n_i - 1) \cdot ln \nobreakspace s_i^2] \end{equation*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-451641096c345ed1a7ce4de96a67b2f3_l3.png)
wobei
![Rendered by QuickLaTeX.com \begin{equation*} C = 1 + \frac 1 {3 \cdot (k-1)} \cdot \left [\sum_{i=1}^k \nobreakspace \frac 1 {n_i-1} - \frac 1 {n-r} \right ] \end{equation*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-3ef7b96db3d8c498d5f40d991a643886_l3.png)
Stell Dir vor, Du möchtest die Schwankungen der Zuhörerzahlen in drei Vorlesungen miteinander vergleichen, für die Du Normalverteilung unterstellen kannst.
Du notierst also die Hörerzahlen in aufeinanderfolgenden Wochen und berechnest für jede Vorlesung die mittlere Hörerzahl und die Stichprobenvarianz:
| Allgemeine VWL | Statistik | Marketing | |||
| 14 | 12 | 15 | |||
| 135,07 | 31,33 | 167,14 | |||
| 491,92 | 254,06 | 504,13 | |||
Als gewichteten Mittelwert der Stichprobenvarianzen erhältst Du daraus: ![]()
Durch Einsetzen in die Formel der Prüfgröße erhältst Du:
![]()
Mit
![]()
verwirfst Du die Nullhypothese nicht, die Varianzen der Grundgesamtheiten seien gleich.
Der Bartlett-Test kann nur angewendet werden, wenn Du Stichproben aus normalverteilten Zufallsvariablen betrachtest; er reagiert empfindlich auf Abweichungen dieser Voraussetzung und Du solltest Dich dann für den robusteren Levene-Test entscheiden. Ist die Voraussetzung der Normalverteilung erfüllt, so besitzt der Bartlett-Test eine größere Trennschärfe als der Levene-Test.
