Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Welch-Test
- 26. April 2018
- Posted by: Mika
Stell Dir vor, Du hast zu den normalverteilten Zufallsvariablen ![]() , i=1,…n, und
, i=1,…n, und ![]() , j=1,…m zwei unabhängige Stichproben erhoben und möchtest einseitige oder zweiseitige Hypothesentests bezüglich der Mittelwerte
, j=1,…m zwei unabhängige Stichproben erhoben und möchtest einseitige oder zweiseitige Hypothesentests bezüglich der Mittelwerte ![]() und
und ![]() durchführen:
durchführen:
![]()
![]()
oder
![]()
![]() .
.
Dann bestimmt Deine Kenntnis über die Grundgesamtheitsvarianzen den einzusetzenden Test:
- Bei bekannter Varianz der Grundgesamtheiten kannst Du den Gauss-Test einsetzen.
- Sind die Varianzen nicht bekannt, können aber als gleich angenommen werden, so ist der t-Test dein geeignetes Instrument.
- Den Fall, dass sich die unbekannten Varianzen der Grundgesamtheit unterscheiden, bezeichnet man als Behrens-Fisher-Problem. Hierfür kannst Du den Welch-Test anwenden.
Du kannst den Welch-Test als modifizierten t-Test beschreiben, bei dem die Varianz der Stichproben-Mittelwertdifferenz aus den Stichprobenvarianzen ermittelt wird:
![]()
Stell Dir vor, Du möchtest die Wuchshöhe in Zentimetern zweier Heckenpflanzen X und Y miteinander vergleichen und erhebst dazu zwei Stichproben:
| X: Thuja | Y: Kirschlorbeer | ||||
| n | m | ||||
| 8 | 152 | 100 | 12 | 158 | 225 |
Für die Differenz der Mittelwerte schätzest Du daraus die Varianz als
![]()
Deine Prüfgröße lautet:
![]()
Deine Prüfgröße folgt unter der Nullhypothese approximativ einer ![]() -Verteilung mit
-Verteilung mit
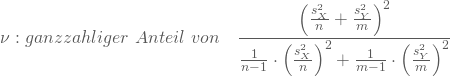
Freiheitsgraden. Hier erhältst Du ![]() . Im Fall des einseitigen Tests
. Im Fall des einseitigen Tests
![]() gegen
gegen ![]()
wird ![]() verworfen, wenn
verworfen, wenn ![]() <
< ![]() .
.
Mit ![]() kannst Du die Nullhypothese nicht verwerfen.
kannst Du die Nullhypothese nicht verwerfen.
Testest Du zweiseitig, etwa
![]() gegen
gegen ![]() ,
,
so verwirfst Du Deine Nullhypothese, wenn ![]() <
< ![]() oder
oder ![]() >
> ![]() .
.
Mit
![]()
wird die zweiseitige Nullhypothese nicht verworfen.
