t-Test

t-Test

  • 26. Januar 2017
  • Posted by: Mika
Keine Kommentare

Der t-Test ermöglicht es Dir, aufgrund der Realisationen Deiner Stichprobe(n) Hypothesen über den oder die Mittelwerte der Grundgesamtheit zu prüfen, wenn Du für die Grundgesamtheit Normalverteilung unterstellen kannst aber die Varianz der Grundgesamtheit nicht kennst. Damit ist dieser Test für Fälle geeignet, für die der Gauß-Test nicht anwendbar ist.

Wie beim Gaußtest lassen sich drei Anwendungsfälle unterscheiden:

Einstichprobentest

Dir liegt eine Stichprobe vor, deren Varianz in der Grundgesamtheit unbekannt ist. Du kannst testen, ob Dein Stichprobenmittelwert mit einem angenommenen Mittelwert der Grundgesamtheit vereinbar ist (zweiseitiger Test) oder ob es systematische Abweichungen nach oben oder nach unten gibt (einseitiger Test).

Angenommen, Du als Reiseunternehmer untersuchst, wie viel Euro Studenten im Jahr für Reisen ausgeben und hast dazu in Köln eine Stichprobe vom Umfang n= 27 erhoben. Diese ergab einen Mittelwert \bar x von 847 Euro und eine Standardabweichung s_x von 100, letztere erwartungstreu geschätzt. Eine ältere Untersuchung ergab einen mittleren Ausgabewert von 750 Euro.

Jetzt möchtest Du testen, ob die Kölner Studenten heute mehr als 750 Euro ausgeben. Du stellst Deine Hypothesen entgegengesetzt zu Deiner Vermutung auf als

    \begin{equation*} H_0: \mu \le 750 \quad und \quad H_1: \mu > 750 \end{equation*}

Für die Teststatistik standardisierst Du den Mittelwert der Stichprobe durch Subtraktion des angenommenen Grundgesamtheitsmittels vom Stichprobenmittelwert und Division der Differenz durch die Standardabweichung der Stichprobe. Die Teststatistik folgt einer t-Verteilung mit \nu = (n-1) Freiheitsgraden.

Mit

    \begin{equation*} \frac { \bar x - \mu} { \frac {s_x} {\sqrt n}}= \frac {847-750} {\frac {100} {\sqrt {27} }} = \frac {97} {19,245} = 5,04 = t_{pr} > t_{(0,95;26)} =1,7056\end{equation*}

verwirfst Du Deine Nullhypothese mit einer Irrtumswahrscheinlichkeit von 5 \% und schließt, dass die Reiseausgaben der jetzigen Kölner Studenten höher sind als bei den Probanden der alten Studie.

Zweistichprobentest für unverbundene Stichproben

Dir liegen zwei Stichproben vor, die beide zu normalverteilten Zufallsvariablen gehören, deren Varianzen der Grundgesamtheit unbekannt sind aber als gleich angenommen werden können: Du kannst jetzt testen, ob die beiden Mittelwerte gleich sind, oder ob es systematische Unterschiede gibt.

Stell Dir vor, Du erhebst eine weitere Stichprobe in Düsseldorf, diesmal vom Umfang n_2=25. Diese ergibt einen Stichprobenmittelwert von \bar x_2 = 853 und ebenfalls eine Standardabweichung von 100.Jetzt kannst Du testen, ob es systematische Unterschiede im Ausgabeverhalten für Reisen der Studenten in Köln und Bonn gibt:

    \begin{equation*} H_0: (\mu_1 - \mu_2) =0 \quad und \quad H_1: (\mu_1 - \mu_2) \ne 0 \end{equation*}

Wenn die standardisierten Mittelwerte der einzelnen Stichproben t-verteilt sind, gilt das auch für deren Differenz, mit \nu=(n_1+n_2-2) Freiheitsgraden, und Du kannst Deine Testentscheidung zum Niveau von 5\% treffen:

    \begin{equation*} \frac { \bar x_1 - \bar x_2} {s_x \cdot \sqrt{\frac 1 {n_1} + \frac 1 {n_2}}} = \frac {-6} {100 \cdot \sqrt { \frac 1 {25} + \frac 1 {27}}} = -0,2162 = t_{pr} > t_{(0,025;50)} =-2,0085 \end{equation*}

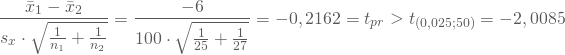
Mit Deinen Stichprobenergebnissen gibt es keinen Grund, die Nullhypothese zu verwerfen und systematische Unterschiede im Ausgabeverhalten der Studenten in den beiden Städten anzunehmen.
Falls die beiden Stichproben unterschiedliche Varianzen besitzen, ist der t-Test nicht anwendbar. Dann greift der Welch-Test als eine Modifikation für diesen Fall.

Zweistichprobentest für verbundene Stichproben

Für jedes i = 1 bis n liegen Paare von Messwerten vor, z.B. „vorher-nachher- Werte“, die Du als normalverteilt annehmen kannst, deren Varianz Du aber nicht kennst. Du testest jetzt, ob die beiden Mittelwerte der Messungen gleich sind oder ob es systematische Abweichungen gibt.

Nach Deiner ersten Erhebung führst Du eine große Werbekampagne für Deine Reiseangebote für junge Leute durch. Ein halbes Jahr nach Deiner ersten Stichprobe in Köln befragst Du Deine Teilnehmer erneut nach ihren Ausgaben für Reisen. Du möchtest prüfen, ob Deine Werbung erfolgreich war, ob sich also das Ausgabeverhalten aufgrund Deiner Werbung erhöht hat. Für jeden der n=27 Probanden liegen Dir also Wertepaare (x_i,y_i) vor, aus denen Du die Differenzen d_i = y_i - x_i bilden kannst. Aus diesen berechnest Du den Mittelwert \bar d = 26,5 und die Standardabweichung der Stichprobe s_d=21.

Du möchtest mit der Irrtumswahrscheinlichkeit von \alpha testen, ob der Mittelwert \mu der Differenzen in der Grundgesamtheit positiv ist. Dazu formulierst Du die Hypothesen umgekehrt zu Deiner Vermutung:

    \begin{equation*} H_0: \mu \le 0 \quad gegen \quad H_1: \mu > 0 \end{equation*}

Die Nullhypothese wird verworfen, falls der Prüfwert zu groß wird:

    \begin{equation*} \frac { \bar d } {{s_d \cdot \frac 1 { \sqrt{n}}}} = \frac {26,5} {21 \cdot 0,192} = 6,572 = t_{pr} > t_{(0,95;26)} =1,7056\end{equation*}

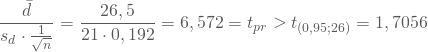
Du kannst also mit einer Irrtumswahrscheinlichkeit von 5% annehmen, dass Deine Werbung erfolgreich war.

Mit steigendem n nähert sich die t-Verteilung der Standardnormalverteilung an:

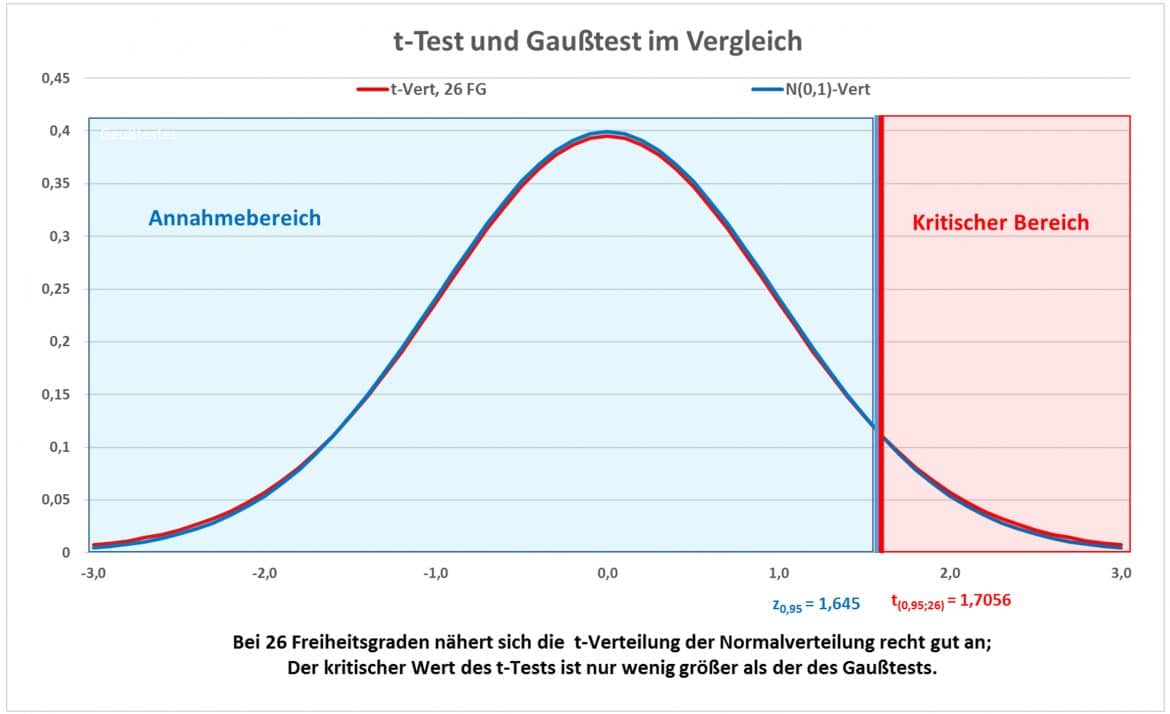
t-test-gauss-test
In der Grafik kannst Du die Annäherung der Verteilungsfunktionen aneinander gut erkennen und auch, dass die kritischen Werte sehr dicht zusammenfallen: Mit zunehmender Stichprobengröße wird die Schätzung der Varianz der Grundgesamtheit aus der Stichprobe immer sicherer und nähert sich an den wahren Wert \sigma an. Für große n sind die Ergebnisse von t-Test und Gaußtest entsprechend sehr ähnlich.