Momentenmethode

Momentenmethode

  • 16. November 2016
  • Posted by: Mika
Keine Kommentare

Die Momentenmethode ist eins der ältesten Verfahren zur Schätzung der Parameter der Grundgesamtheit aus einer Stichprobenerhebung. Sie ist ohne viel Rechenaufwand durchzuführen, liefert Dir aber nicht immer erwartungstreue Schätzfunktionen.

Theoretische Momente

Als k-tes theoretisches Moment m_k einer Zufallsvariablen X_i ist der Erwartungswert der k-ten Potenz von X_i definiert, m_1 beispielsweise ist der Erwartungswert von X_i, m_2 der von X_i^2:

    \begin{equation*} m_k= E(X_i^k)\end{equation*}

Die theoretischen Momente hängen natürlich von den wahren unbekannten Parametern der Grundgesamtheit ab, für die Normalverteilung beispielsweise von den Parametern \mu und \sigma^2, und Du kannst die m_k als deren Funktionen formulieren:

    \begin{equation*} m_1= E(X_i)= \mu \quad und \quad m_2 = E(X_i^2) = Var(X_i^2) + [E(X_i)]^2 = \sigma^2 + \mu^2 \end{equation*}

Empirische Momente

Die empirischen Momente \hat m_k dagegen berechnest Du aus den Realisationen Deiner Stichprobe direkt:

    \begin{equation*} \hat m_k= \frac 1 n \cdot \sum_{i=1}^{n} x_i^k\end{equation*}

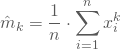
\hat m_1 zum Beispiel als erstes Moment ist der empirische Mittelwert der Stichprobe.
Idee der Momentenmethode ist es, die bekannten empirischen Momente mit den unbekannten theoretischen Momenten gleichzusetzen:

    \begin{equation*} m_j = \hat m_j \quad f\"ur \quad j = 1,...m \end{equation*}

Erwartungstreue: Beispielrechnung

Stell Dir vor, Du betrachtest allgemein eine Verteilung mit m Parametern. Nimmst Du jeweils die ersten m theoretischen und empirischen Momente und setzt sie gleich, so erhältst Du m Gleichungen mit m Unbekannten. Dann löst Du dieses Gleichungssystem nach den m Parametern (falls eindeutig möglich) und erhältst als Lösung ihre Momentenschätzer.
Die Normalverteilung beispielsweise hat zwei Parameter, \mu und \sigma^2, daher betrachtest Du die ersten beiden Momente:

Theoretisches erstes und zweites Moment für die Normalverteilung

    \begin{equation*} m_1 = \hat m_1 : \quad \hat \mu = \frac 1 n \cdot \sum_{i=1}^{n} x_i \end{equation*}

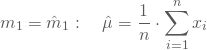
und

    \begin{equation*} m_2 = \hat m_2 :\quad \hat \sigma^2 + \hat \mu^2= \frac 1 n \cdot \sum_{i=1}^{n} x_i^2 \end{equation*}

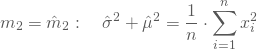
Setzt Du dann in die zweite Gleichung die Schätzfunktion von \hat \mu ein und löst nach \hat \sigma^2 auf, erhältst Du

    \begin{equation*} \hat \sigma^2 = \frac 1 n \cdot \sum_{i=1}^n (x_i - \bar x)^2. \end{equation*}

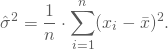
Empirisches erstes und zweites Moment

Stellt Dir jetzt vor, Du hast eine kleine Stichprobe aus der normalverteilten Grundgesamtheit „Körpergröße bei Männern“ gezogen und Deine der Größe nach geordneten Stichprobenrealisationen liegen wie in der zweiten Spalte der Tabelle vor.

Aus diesen Realisationen berechnest Du im Folgenden die beiden ersten empirischen Momente.

i x_i x_i^2
1 1,68 2,82
2 1,74 3,03
3 1,75 3,06
4 1,82 3,31
5 1,83 3,35
6 1,95 3,8
Summe 10,77 19,37
k-tes empirisches Moment \hat m_1 =1,79 \hat m_2=3,23

Setzt Du diese Zahlen dann in die obigen Formeln ein, so erhältst Du:

    \begin{equation*} \hat \mu = \hat m_1 = 1,79 \quad und \quad \hat \sigma^2 + \hat \mu^2 = \hat m_2= 3,23 \end{equation*}

Als Schätzwert für die Varianz erhältst Du schließlich durch Einsetzen und Umformen \hat \sigma^2 = 0,026.

Dem Vorteil der sehr einfachen Berechnung steht der Nachteil gegenüber, dass die Schätzfunktionen nicht immer erwartungstreu sind, wie hier zum Beispiel die Schätzfunktion für die Varianz, bei der erst durch den Bessel´sche Korrekturfaktor \frac {n} {n-1} Erwartungstreue erreicht werden kann.