Maximum-Likelihood-Methode

Maximum-Likelihood-Methode

  • 16. November 2016
  • Posted by: Mika
Keine Kommentare

Die Maximum-Likelihood-Methode ist ein parametrisches Schätzverfahren, mit dem Du die Parameter der Grundgesamtheit aus der Stichprobe schätzt. Idee des Verfahrens ist es, als Schätzwerte für die wahren Parameter der Grundgesamtheit diejenigen auszuwählen, unter denen die beobachteten Stichprobenrealisationen am wahrscheinlichsten sind. Daher auch der Name des Verfahrens.

Stell Dir beispielsweise vor, Du möchtest wissen, wie hoch der Prozentsatz der Erstsemesterstudenten des Fachs Betriebswirtschaftslehre ist, die bereits mindestens ein Praktikum absolviert haben. Aus den 400 Studenten erhebst Du zuerst eine Stichprobe vom Umfang 30 und befragst sie. Zwölf Studenten geben Praktikumserfahrung an, die übrigen 18 sind noch unerfahren.

Wahrscheinlichkeiten der Binomialverteilung

Jetzt betrachtest Du die Wahrscheinlichkeit der Binomialverteilung, genau 12 aus 30 Studenten mit Praktikumserfahrung vor Dir zu haben, in Abhängigkeit von dem unbekannten Anteilswert der Grundgesamtheit:

Anteilswert p 
in der Grundgesamtheit Wahrscheinlichkeit für genau 12 aus 30 Studenten bei einem Anteilswert von p
Wahrscheinlichkeiten der Binomialverteilung
20% 0,60%
25% 2,90%
30% 7,50%
35% 12,50%
40% 14,70%
45% 12,60%
50% 8,10%

Mit 14,7 % ist also die Wahrscheinlichkeit, Dein beobachtetes Stichprobenergebnis zu beobachten, bei einem Anteilswert von 40% in der Grundgesamtheit am höchsten. Damit ist dieser Dein Maximum-Likelihood-Schätzer.

Likelihood-Funktion

Im Allgemeinen bildest Du eine Likelihood-Funktion L als Wahrscheinlichkeitsfunktion, genau die Stichprobenrealisationen x_1 bis x_n zu erhalten, in Abhängigkeit von den unbekannten Parametern \Delta der Grundgesamtheit.

    \begin{equation*} L = L(x_1, …x_n| \Delta) = f(x_1| \Delta) \cdot f(x_2| \Delta) \cdot ...f(x_n| \Delta) \cdot = \prod_{i=1}^{n} f(x_i| \Delta) \end{equation*}

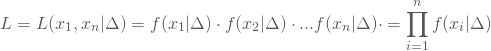
Dann maximierst Du diese Funktion, indem Du sie nacheinander nach allen Komponenten von \Delta differenzierst und die Ableitungen mit Null gleichsetzt. Im Fall der Normalverteilung beispielsweise mit den beiden Parametern \mu und \sigma^2, erhältst Du zwei Gleichungen mit zwei Unbekannten:

    \begin{equation*} \frac {\partial L }{\partial \mu} = 0 \quad und \quad \frac {\partial L }{\partial \sigma^2} =0 \end{equation*}

Die Lösung dieser beiden Gleichungen liefert folglich Deine Maximum-Likelihood-Schätzer

    \begin{equation*} \hat \mu =\frac {1} {n}\sum_{i=1}^n x_i \quad und \quad \hat \sigma^2 = \frac {1} {n} \sum_{i=1}^n (x_i - \bar x)^2 \end{equation*}

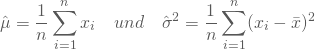
Die Schätzfunktionen aus der Maximum-Likelihood-Methode sind nicht immer erwartungstreu. Im Fall der Schätzfunktion für \sigma^2 beispielsweise ist auch hier der Bessel´sche Korrekturfaktor \frac {n} {n-1} erforderlich, wie bei der Momentenmethode.

Falls es eine Lösung gibt, ist sie aber immer effizient.