Konfidenzintervall für Erwartungswert, Varianz und Median

Konfidenzintervall für Erwartungswert, Varianz und Median

  • 16. November 2016
  • Posted by: Mika
Keine Kommentare

Hast Du für Deine Schätzung der Grundgesamtheit eine geeignete Stichprobe erhoben, so kannst Du daraus Schätzungen für die Parameter der Grundgesamtheit vornehmen. Solche Parameter sind z. B. der Erwartungswert, die Varianz oder der Median.

Diese Werte sind Punktschätzungen. Sie stimmen mit nur sehr geringer Wahrscheinlichkeit exakt mit den Parametern der Grundgesamtheit überein. Dies gilt selbst dann wenn sie alle statistisch wünschenswerten Eigenschaften aufweisen. Es ist daher interessant zu ermitteln, in welchem Zahlenbereich sich der wahre Parameter befindet.

Was ist ein Konfidenzintervall?

Ein Konfidenzintervall oder auch Vertrauensintervall ist ein aus einer Stichprobe mithilfe der Schätztheorie bestimmter Intervallbereich. In diesem Bereich liegen die Parameter der Grundgesamtheit dann mit einer bestimmten Wahrscheinlichkeit. Dabei sind die Grenzen des Intervalls Zufallsvariablen.
Im Zuge einer Untersuchung des Ausgabeverhaltens von Studenten in Deutschland hast Du beispielsweise eine geeignete Stichprobe vom Umfang n=200 gezogen. Die Ausgaben für Nahrungsmittel hast Du dabei wie folgt erfragt: „Wieviel Euro gibst Du im Monat für Nahrungsmittel aus?“
Die Auswertung der Antworten ergaben dann die folgenden Schätzwerte für die wahren Parameter:

  • Mittlere Ausgaben 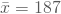 \bar{x}=187 als Schätzwert für den Erwartungswert
  • Stichprobenvarianz: 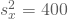s_x^2=400, Standardabweichung: 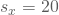s_x=20 als Schätzwerte für die Varianz 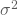\sigma^2 bzw. der Standardabweichung σ der Grundgesamtheit
  • Median: 185

Um diese Schätzwerte suchst Du nun symmetrische Intervalle, in denen die wahren Parameterwerte mit einer Wahrscheinlichkeit von 95% liegen.

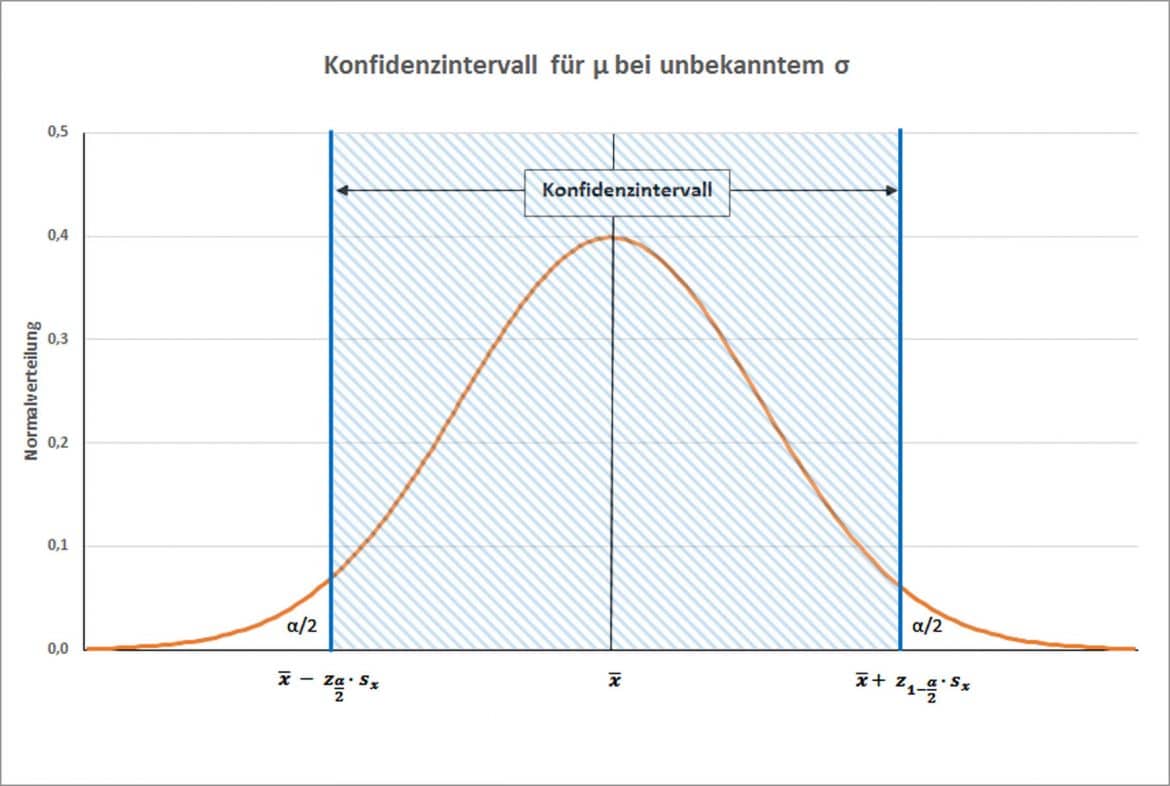
Konfidenzintervall für den Erwartungswert E(X)

    \begin{equation*} Prob\{x_u\leq E(X) \leq x_0\}=0,95 \end{equation*}

Bei großen Stichproben, etwa ab n=100, kannst Du E(X) gemäß dem Zentralen Grenzwertsatz als normalverteilt ansehen. Du transformierst dann alles in standardnormalverteilte Werte.
Die standardisierten Grenzen des 95%-Konfidenzintervalls ergeben sich dann als z-Werte der Standardnormalverteilung an den Stellen 2,5% und 97,5%:

    \begin{equation*} z_{0,025}=F^{-1}(0,025)=-1,960 \quad \text{und} \quad z_{0,975}=F^{-1}(0,975)=1,960 \end{equation*}

Aus diesen standardisierten Werten kannst Du die anschließend die Intervallgrenzen durch Rückgängigmachen der Standardisierung berechnen:

    \begin{equation*} x_u=\bar{x} + z_u\cdot s_x \quad \text{und} \quad x_0=\bar x + z_0\cdot s_x \end{equation*}

konfidenzintervall-normalverteilung

Einsetzen der Zahlen ergibt dann die untere und obere Grenze Deines Konfidenzintervalls.

    \begin{equation*} x_u=\bar{x} + z_u\cdot s_x \quad \text{und} \quad x_0=\bar x + z_0\cdot s_x \end{equation*}

Mit einer Wahrscheinlichkeit von 95% haben die Daten ein Konfidenzintervall geliefert, das den wahren Mittelwert enthält. Der Erwartungswert der monatlichen Ausgaben von Studenten für Nahrungsmittel liegt also zwischen 147,80 € und 226,20 €.
Für kleine Stichproben mit n < 100 kannst Du dagegen keine Normalverteilung annehmen. Dann folgt die standardisierte Zufallsvariable einer t-Verteilung mit \nu=n-1 Freiheitsgraden. Für die Berechnung der Grenzen des Konfidenzintervalls tritt dann an die Stelle der z-Werte die entsprechenden Werte der t-Verteilung.

Konfidenzintervall für die Varianz 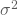\sigma^2

Hier nutzt Du anstelle der Normalverteilung aus, dass der Quotient aus Stichprobenvarianz und Varianz der Grundgesamtheit einer  \chi^2 -Verteilung mit \nu=n-1 Freiheitsgraden folgt.

Es ergibt sich also:

    \begin{equation*} Prob\left\{\frac{(n-1)S_x^2}{\chi^2_{(\nu;1-\frac{\alpha}{2})}}\leq\sigma^2\leq\frac{(n-1)S_x^2}{\chi^2_{(\nu;\frac{\alpha}{2})}}\right\}=0,95 \end{equation*}

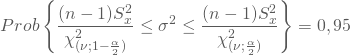
Du settzt in diese allgemeine Formel Deine Stichprobenschätzwerte und die Werte der Verteilung ein. Damit erhältst Du als untere und obere Grenzen des Konfidenzintervalls für die Varianz:

    \begin{equation*} \frac{(n-1)S_x^2}{\chi^2_{(\nu;1-\frac{\alpha}{2})}}=\frac{199\cdot 400}{239,96}=331,72 \quad \text{und} \quad \frac{(n-1)S_x^2}{\chi^2_{(\nu;\frac{\alpha}{2})}}=\frac{199\cdot 400}{161,83}=491,87 \end{equation*}

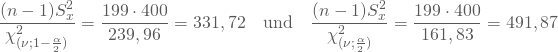
Das Konfidenzintervall mit den Grenzen 331,72 und 491,87, das die Stichprobe geliefert hat, enthält folglich Deine wahre Varianz mit einer Wahrscheinlichkeit von 95%.

Konfidenzintervall für den Median

Im Fall einer großen Stichprobe mit n\geq 100 kann die Verteilung von X und E(X) als asymptotisch normalverteilt angesehen werden. Die Normalverteilung ist symmetrisch. Das bedeutet, dass Erwartungswert und Median zusammenfallen. Das Konfidenzintervall für den Median ist dann identisch mit dem für den Erwartungswert.

Im Fall einer kleinen Stichprobe und unbekannter Verteilung der Grundgesamtheit bieten Statistikprogramme dennoch Optionen an. Du kannst so mittels Bootstrapping-Verfahren meist asymmetrische Konfidenzintervalle für den Median ermitteln.