Histogramm

Ein Histogramm liefert Dir die grafische Darstellung der absoluten oder relativen Häufigkeitsverteilung eines quantitativen, klassierten Merkmals in einem speziellen Säulendiagramm: Der Flächeninhalt der einzelnen (aneinandergrenzenden) Säulen gibt die Häufigkeit der jeweiligen Klassen wider, die Höhe der Säulen steht für die Häufigkeitsdichte der Klasse. Damit erhältst Du also mehr Informationen als es ein Säulendiagramm zu liefern vermag.

Die Einkommen von 100 Personen im Alter zwischen 20 und 30 Jahren wurden erhoben und wie in der Tabelle angegeben aufgelistet:

Person	1	2	3	…
Einkommen	5.653 €	15.364 €	22.546 €	…

Zuerst teilst Du die möglichen Merkmalsausprägungen in k sinnvolle Klassen auf, die unterschiedlich breit sein dürfen. Allerdings vereinfacht eine gleiche Klassenbreite zumindest im mittleren Wertebereich die Interpretation der Grafik.

Bestimmung von Häufigkeiten

Für jede Klasse ermittelst Du zuerst die absolute (oder relative) Häufigkeit, mit der diese Klasse beobachtet wurde. Den Flächeninhalt einer Säule (=Rechteck) bestimmst Du durch das Produkt von Breite mal Höhe. Außerdem hast Du Klassenbreite und Flächeninhalt als Häufigkeit vorliegen. Also kannst Du die Höhe der Säule als Quotient von Flächeninhalt und Klassenbreite berechnen. Die Höhe der Säule entspricht dann der Häufigkeitsdichte der Klasse.

Einkommenshäufig bei 15 Personen im Alter zwischen 20 und 30 Jahren
Klasse i	von …	bis unter …	Klassenbreite	Dichte:
1	3000	10000	7000	1	0,000142857
2	10000	20000	10000	24	0,0024
3	20000	30000	10000	19	0,0019
4	30000	40000	10000	23	0,0023
5	40000	50000	10000	12	0,0012
6	50000	70000	20000	15	0,00075
7	70000	90000	20000	6	0,0003

 

Das Histogramm ergibt sich zu: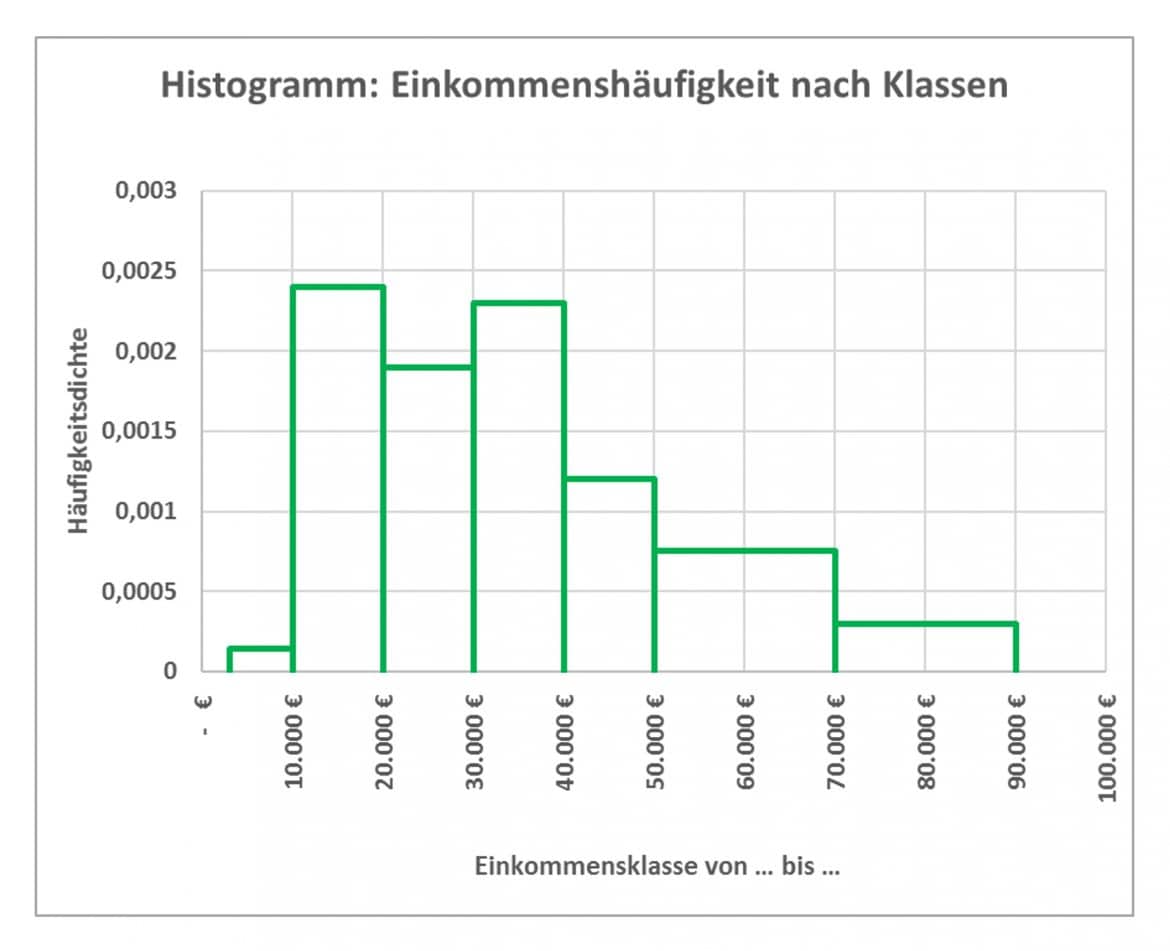

Du erkennst gut die schmalere Klassenbreite im unteren und die größere Klassenbreite im oberen Einkommensbereich. Der Flächeninhalt der Säulen entspricht der Häufigkeit der jeweiligen Klasse.