Spearmans Rangkorrelationskoeffizient (Spearmans R)

Spearmans Rangkorrelationskoeffizient (Spearmans R)

  • 30. Oktober 2017
  • Posted by: Mika
Keine Kommentare

Spearmans Rangkorrelationskoeffizient ist eine Erweiterung des Korrelationskoeffizienten nach Bravais Pearson, der metrisches Datenmaterial unterstellt und zudem auf linearen Zusammenhang begrenzt ist. Indem Du die Berechnungen des Korrelationskoeffizienten auf die Ränge der Beobachtungswerte anwendest, kannst Du ihn auf ordinalskalierte Daten anwenden, die beliebig zusammenhängen.

Die Teilnehmer einer Abnehmstudie werden beispielsweise nach sechs Wochen gefragt, wie zufrieden sie mit dem von ihnen angewendeten Programm sind. Neben dem Grad der Zufriedenheit wird das verlorene Gewicht in kg dokumentiert und Du möchtest untersuchen, ob ein Zusammenhang zwischen dem Grad der Zufriedenheit und dem Gewichtsverlust besteht.

Beispieldaten

Person X:
Zufriedenheit auf einer Skala von 1 bis 10		 rg(X):
Rang von X		 Y:
Gewichtsverlust
in kg		 rg(Y):
Rang von Y
Teilnehmer 1 8,5 3 8,2 2
Teilnehmer 2 3,0 10 2,0 10
Teilnehmer 3 10,0 1 6,7 3
Teilnehmer 4 6,0 5,5 5,7 4
Teilnehmer 5 5,0 8 3,5 7
Teilnehmer 6 9,5 2 4,8 6
Teilnehmer 7 7,5 4 3,2 8
Teilnehmer 8 6,0 5,5 8,5 1
Teilnehmer 9 4,0 9 2,8 9
Teilnehmer 10 5,5 7 4,9 5
mittlerer Rang 5,5 5,5

Falls Bindungen vorkommen, d.h. wenn der gleiche Wert mehrmals auftaucht, so werden die Rangwerte gemittelt: Beim Grad der Zufriedenheit beispielsweise taucht der Wert 6 zweimal auf. Zu vergeben wären an der Stelle folglich die Ränge 5 und 6; also bekommen beide Werte den Rang 5,5 zugewiesen. Aus diesen Rangwerten wird der Korrelationskoeffizient dann wie gewohnt berechnet:

mit

    \begin{equation*} cov(rg(x),rg(y)) = \frac 1 n \displaystyle\sum_{i=1}^n (rg(x)_i - \bar {rg}(x)) \cdot (rg(y_i) - \bar {rg}(y)) \end{equation*}

    \begin{equation*} s_{rg(x)}= \frac 1 n \displaystyle\sum_{i=1}^n (rg(x)_i - \bar {rg}(x))^2 \quad \end{equation*}

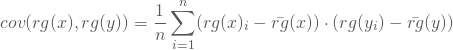
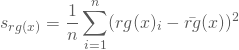
und

    \begin{equation*} s_{rg(y)}= \frac 1 n \displaystyle\sum_{i=1}^n (rg(y)_i - \bar {rg}(y))^2 \end{equation*}

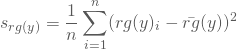
Für Dein Beispiel erhältst Du dann:

i rg(x): rg(y): (rg(x)_i-\bar {rg}(x)) (rg(y)_i-\bar {rg}(y)) (rg(x)_i-\bar {rg}(x))^2 (rg(y)_i-\bar {rg}(y))^2 (rg(x)_i-\bar {rg}(x)) \cdot(rg(y)_i-\bar {rg}(y))$
1 3 2 -2,50 -3,50 6,25 12,25 8,75
2 10 10 4,50 4,50 20,25 20,25 20,25
3 1 3 -4,50 -2,50 20,25 6,25 11,25
4 5,5 4 – -1,50 – 2,25 0,00
5 8 7 2,50 1,50 6,25 2,25 3,75
6 2 6 -3,50 0,50 12,25 0,25 -1,75
7 4 8 -1,50 2,50 2,25 6,25 -3,75
8 5,5 1 – -4,50 – 20,25 0,00
9 9 9 3,50 3,50 12,25 12,25 12,25
10 7 5 1,50 -0,50 2,25 0,25 -0,75
Summe 82,00 82,50 50,00
Mittelwert 5,5 5,5 5,20 – 8,20 8,25 5,00

Einsetzen in die Formel

    \begin{equation*} r_S = \frac { cov(rg(x),rg(y))} { s_{ rg(x)} \cdot s_{ rg(y)}} = \frac {5,55 } {\sqrt {9,11} \cdot \sqrt {9,17} } =0,6079 \end{equation*}

Also lassen sich 60,79 Prozent der Streuung in den Rangwerten von Gewichtsverlust und Grad der Zufriedenheit durch den Zusammenhang zwischen beiden erklären.