Korrelationskoeffizient

Korrelationskoeffizient

  • 30. Oktober 2017
  • Posted by: Mika
Keine Kommentare

Die Kovarianz zwischen zwei metrisch skalierten Merkmalen als das mittlere Produkt der Abweichungen beider Merkmale von ihrem Mittelwert ist ein Maß für den linearen Zusammenhang zwischen den Merkmalen. Allerdings eignet sie sich nur sehr bedingt für den Vergleich. Denn ihr betragsmäßiger Wert ist von der Größenordnung der Ausgangsmerkmale abhängig.

Der Korrelationskoeffizient r_{xy} nach Bravais und Pearson greift diese Problematik auf, indem er die Kovarianz aus den standardisierten Werten berechnet: Du berechnest für jedes Merkmal seinen Mittelwert und die Standardabweichung. Dann subtrahierst Du von jedem Beobachtungswert den Mittelwert dieses Merkmals und dividierst die Differenz durch die Standardabweichung. Dadurch normierst Du den Wert der Kovarianz auf den Bereich zwischen minus eins und plus eins.

    \begin{equation*} r_{x,y} = \frac { cov(x,y)} {\sqrt {s^2_x \cdot s^2_y}} = \frac 1 n \sum _{i=1}^n x_i^* \cdot y^*_i , \quad mit \quad x_i^* = \frac {x_i - \bar x } {s_x} \quad und \quad y_i^* = \frac {y_i - \bar y } {s_y} und \quad s_x = \sqrt {\frac 1 n \displaystyle\sum _{i=1}^n (x_i - \bar x)^2 } \quad sowie \quad s_y = \sqrt {\frac 1 n \displaystyle\sum _{i=1}^n (y_i - \bar y)^2 } \quad \end{equation*}

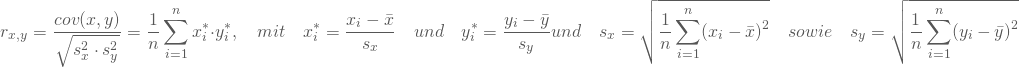
Was gibt der Korrelationskoeffizient an?

Der Wert des Korrelationskoeffizienten gibt Dir dann den prozentualen Anteil der Streuung der Werte an, der durch einen linearen Zusammenhang zwischen beiden Merkmalen erklärt wird:

Ein Korrelationskoeffizient von Null lässt auf fehlenden Zusammenhang schließen. Liegt der Wert dagegen in der Nähe von (minus) eins, gibt er Dir an, dass ein sehr starker positiver (negativer) Zusammenhang zwischen den Merkmalen besteht.

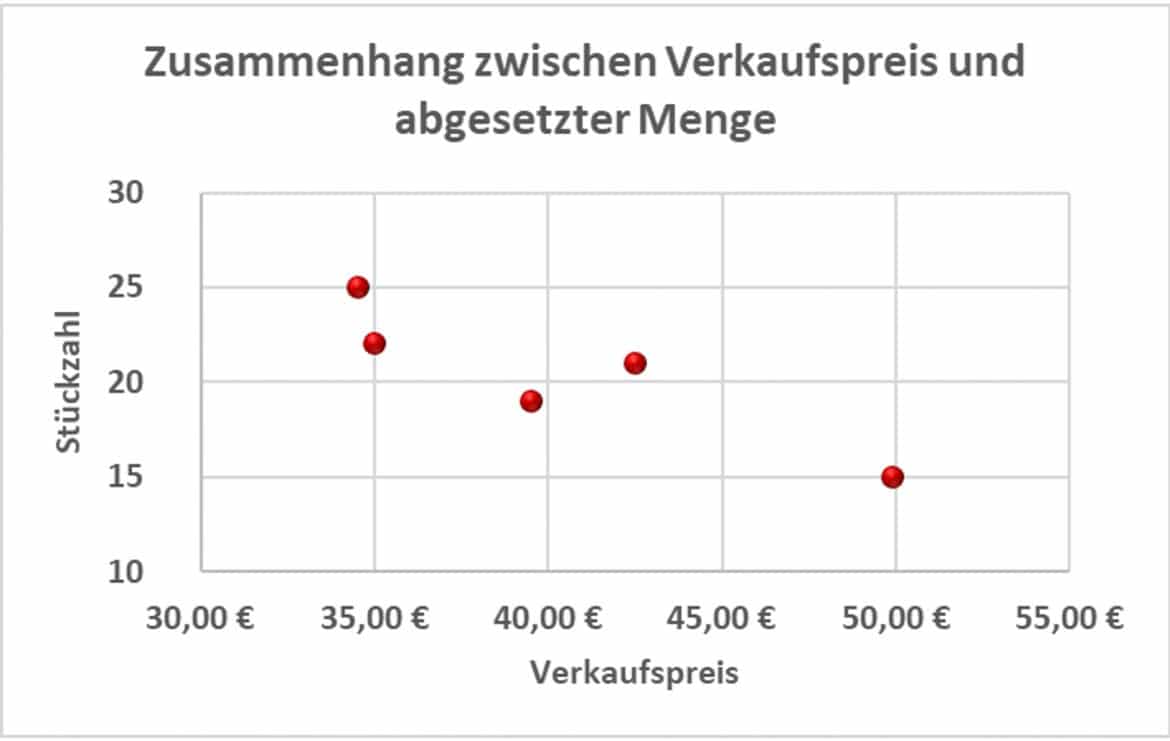
Stell Dir vor, Du arbeitest daran, ein neues Parfum auf den Markt zu bringen. Für die Preisfestsetzung möchtest Du anhand von Testverkäufen in fünf ausgewählten Parfümerien untersuchen, wie stark der Preis die Verkaufszahlen beeinflusst. Du erhältst die folgende Tabelle:

lfd. Nr. Verkaufs- preis in Euro Stück- zahl standardisierte Werte Produkt der stand. Werte
i x_i y_i x_i^* y_i^* x_i^* cdot y_i^*
1 35,00 22 -0,93523 0,48154 -0,45035
2 39,50 19 -0,13816 -0,42135 0,05821
3 42,50 21 0,39322 0,18058 0,07101
4 49,90 15 1,70396 -1,62521 -2,76929
5 34,50 25 -1,02379 1,38444 -1,41738
Mittelwert 40,28 20 0,0 0,0 -0,90156
Standard-abweichung 5,65 3,32 1,00 1,00

Dein Korrelationskoeffizient zwischen der verkauften Stückzahl und dem Verkaufspreis ergibt sich als Durchschnitt der Produkte der standardisierten Beobachtungswerte zu -0,90156. Die verkaufte Menge lässt sich also zu 90,156 Prozent durch den Preis erklären.

Die Grafik zeigt die enge negative Abhängigkeit zwischen Preis und verkaufter Stückzahl:

Korrelationskoeffizient