Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Kontingenzkoeffizient nach Pearson
- 30. Oktober 2017
- Posted by: Mika
Der Kontingenzkoeffizient nach Pearson ist ein Maß für den Zusammenhang zwischen zwei Merkmalen beliebigen Skalenniveaus, wobei für die Art des Zusammenhangs keine Annahmen getroffen werden.
Stell Dir zum Beispiel vor Du arbeitest für eine Kaffeekette und möchtest den Zusammenhang zwischen dem Geschlecht und der Auswahl des Heißgetränks messen. Dazu notierst Du bei n=100 Kunden jeweils das Geschlecht und Ihre Bestellung und erstellst aus den Häufigkeiten ![]() die folgende Kreuztabelle:
die folgende Kreuztabelle:
| Heißgetränk Geschlecht |
Filterkaffee | Cappuccino | Latte Machiato | Summe | |
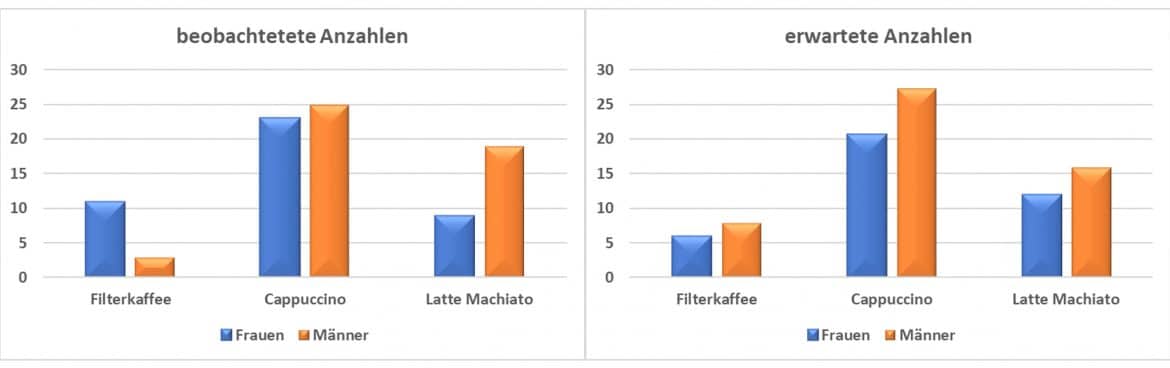
| Frauen | 11 | 23 | 9 | 43 | |
| Männer | 3 | 25 | 19 | 57 | |
| Summe | 14 | 48 | 28 | 100 |
Diesen beobachteten Häufigkeiten ![]() stellst Du die zu erwartenden Häufigkeiten
stellst Du die zu erwartenden Häufigkeiten ![]() gegenüber, die beobachtet würden, falls kein Zusammenhang zwischen Geschlecht und der Getränkewahl besteht: wenn die beiden Merkmale unabhängig voneinander sind, kannst Du die Einzelhäufigkeiten als Produkt der Randhäufigkeiten, dividiert durch die Anzahl n berechnen:
gegenüber, die beobachtet würden, falls kein Zusammenhang zwischen Geschlecht und der Getränkewahl besteht: wenn die beiden Merkmale unabhängig voneinander sind, kannst Du die Einzelhäufigkeiten als Produkt der Randhäufigkeiten, dividiert durch die Anzahl n berechnen:
![]()
Aufstellen einer Unabhängigkeitstabelle
| Heißgetränk Geschlecht |
Filterkaffee | Cappuccino | Latte Machiato | Summe | |
| Frauen | 6,02 | 20,64 | 12,04 | 43 | |
| Männer | 7,98 | 27,36 | 15,96 | 57 | |
| Summe | 14 | 48 | 28 | 100 |
Falls kein Zusammenhang zwischen Geschlecht und Getränkewahl besteht, dürftest Du kaum Abweichungen zwischen den beobachteten ![]() und den erwarteten
und den erwarteten ![]() feststellen; je größer die Abweichungen sind, umso stärker ist der Zusammenhang zwischen beiden.
feststellen; je größer die Abweichungen sind, umso stärker ist der Zusammenhang zwischen beiden.
Die Grafik stellt die beobachteten und erwarteten Häufigkeiten gegenüber:
Berechnung des Kontingenzkoeffizienten
Als Maß für den Zusammenhang kannst Du zuerst den ![]() – oder Kontingenzkoeffizienten als Summe der quadrierten Differenzen, jeweils zur Normierung dividiert durch die erwarteten Häufigkeiten, berechnen:
– oder Kontingenzkoeffizienten als Summe der quadrierten Differenzen, jeweils zur Normierung dividiert durch die erwarteten Häufigkeiten, berechnen:
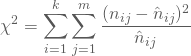
Für Dein Beispiel erhältst Du ![]() .
.
Je kleiner der Koeffizient ausfällt, umso geringer ist der Zusammenhang zwischen den beiden Merkmalen und umgekehrt. Da er jedoch abhängig von der Anzahl der Merkmalsausprägungen und der Beobachtungen ist, ist sein absoluter Wert wenig aussagekräftig und schlecht zum Vergleich geeignet. Deshalb schlug Pearson einen normierten Kontingenzkoeffizienten vor.
Normierter Kontingenzkoeffizient
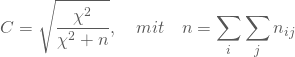
Du erhältst:
![]()
Der Koeffizient C nimmt Werte zwischen Null und Eins an. Daher kann man ihn als normierten ![]() -Koeffizienten interpretieren. Sein Wert bleibt aber definitionsgemäß auch im Fall eines sehr starken Zusammenhangs immer kleiner als Eins; der maximale Wert von C ist durch die kleinere Anzahl der Merkmalsausprägungen bestimmt, wobei m und k für die Anzahl der beiden Merkmalsausprägungen steht:
-Koeffizienten interpretieren. Sein Wert bleibt aber definitionsgemäß auch im Fall eines sehr starken Zusammenhangs immer kleiner als Eins; der maximale Wert von C ist durch die kleinere Anzahl der Merkmalsausprägungen bestimmt, wobei m und k für die Anzahl der beiden Merkmalsausprägungen steht:
![]()
Für Dein Beispiel ergibt sich:
![]()
Korrigierter Kontingenzkoeffizient
Dividierst Du anschließend den Koeffizienten C durch ![]() , so erhältst Du einen korrigierten Kontingenzkoeffizienten, der theoretisch alle Werte im Intervall zwischen Null und Eins annehmen kann, wie für Zusammenhangmaße üblich.
, so erhältst Du einen korrigierten Kontingenzkoeffizienten, der theoretisch alle Werte im Intervall zwischen Null und Eins annehmen kann, wie für Zusammenhangmaße üblich.
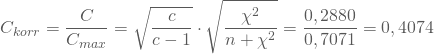
Der korrigierte Kontingenzkoeffizient zwischen dem Geschlecht und der Getränkewahl in Deinem Beispiel beträgt also mit 0,4074 etwa 40 Prozent.
