Chi-Quadrat-Koeffizient

Chi-Quadrat-Koeffizient

  • 30. Oktober 2017
  • Posted by: Mika
Keine Kommentare

Der Chi-Quadrat-Koeffizient ist ein Maß für den Zusammenhang zweier Merkmale beliebigen Skalenniveaus. Er vergleicht beobachtete Häufigkeiten mit im Fall von Unabhängigkeit theoretisch zu erwartenden Häufigkeiten.

Ein neues Deodorant wird beispielsweise in den Duftnoten Mandarine, Zitrone, Vanille, Zimt und Natur angeboten. Um die Werbestrategie optimal auf die jeweilige Zielgruppe anzupassen, sollst Du den Zusammenhang zwischen Duftnote und der Altersgruppe der Probanden messen. Dazu untersuchst Du die Kaufentscheidungen von 200 Testkäufern, die in der folgenden Tabelle aufgeführt sind:

Duftnote Altersgruppe Mandarine Zitrone Vanille Zimt Natur Summe
n_{ij} n_{1j} n_{2j} n_{3j} n_{4j} n_{5j} n_{\cdot j}
unter 40 Jahren n_{i1} 35 14 9 29 35 122
40 Jahre und älter n_{i2} 21 24 5 9 19 78
Summe n_{i \cdot } 56 38 14 38 54 200

Diesen beobachteten Häufigkeiten n_{ij} stellst Du die zu erwartenden Häufigkeiten \hat n_{ij} gegenüber, die beobachtet würden, falls kein Zusammenhang zwischen der Altersgruppe und der ausgewählten Duftnote besteht.

Diese theoretischen Häufigkeiten berechnest Du, indem Du das Produkt der Randhäufigkeiten durch die Anzahl n dividierst:

    \begin{equation*} \hat n_{ij} = \frac {n_{i \cdot} \cdot n_{ \cdot j}} n \end{equation*}

Aufstellen der Unabhängigkeitstabelle

Duftnote Altersgruppe Mandarine Zitrone Vanille Zimt Natur Summe
\hat n_{ij} \hat n_{1j} \hat n_{2j} \hat n_{3j} \hat n_{4j} \hat n_{5j} \hat n_{\cdot j}
unter 40 Jahren \hat n_{i1} 34,16 23,18 8,54 23,18 32,94 122
40 Jahre und älter \hat n_{i2} 21,84 14,82 5,46 14,82 21,06 78
Summe \hat n_{i \cdot } 56 38 14 38 54 200

Je stärker sich die beobachteten Häufigkeiten von den theoretisch zu erwartenden unterscheiden, umso stärker ist der Zusammenhang zwischen beiden Merkmalen. In der Grafik kannst Du beobachtete und erwartete Anzahlen vergleichen:

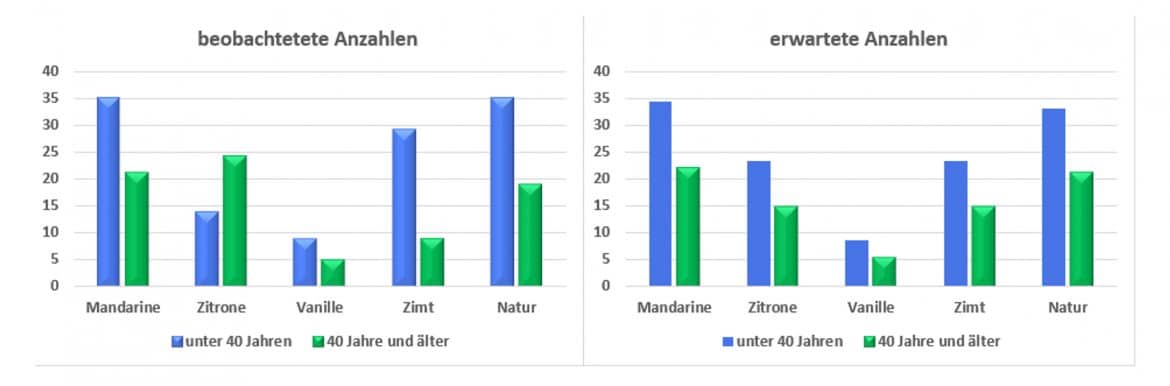
Chiquadrat

Chi-Quadrat-Koeffizient: So wird er berechnet

Für die Berechnung des Qui-Quadrat-Koeffizienten quadrierst Du die Differenzen zwischen den n_{ij} und den \hat n_{ij}, dividierst zur Normierung durch die erwarteten Häufigkeiten und summierst über alle i und alle j:

    \begin{equation*} \chi^2 = \sum_{i=1}^k \sum_{j=1}^m \frac { (n_{ij} -{\hat n_{ij})^2}} {\hat n_{ij}} \end{equation*}

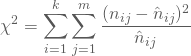
Einsetzen der Werte Deiner Tabellen ergibt folglich \chi^2 =13,5156.

Dieser Wert ist schwer zu interpretieren. Er bestätigt zwar die auch durch die Grafik nahegelegte Vermutung, dass ein Zusammenhang zwischen den Duftnoten besteht, wie stark dieser aber im Vergleich mit anderen Untersuchungen zu bewerten ist, ist allerdings schwer zu sagen. Denn seine Höhe hängt maßgeblich von der Anzahl der Merkmalsausprägungen und der Beobachtungen ab.

Diese Problematik greifen sowohl der Kontingenzkoeffizient nach Pearson als auch Cramérs V auf. Beide Verfahren normieren den Chi-Quadrat-Koeffizienten auf unterschiedliche Weise auf den Bereich zwischen Null und Eins.