Stichprobenvarianz (empirische Varianz)

Stichprobenvarianz (empirische Varianz)

  • 7. September 2017
  • Posted by: Mika
Keine Kommentare

Unter der Stichprobenvarianz versteht man die durchschnittliche quadratische Abweichung der Beobachtungswerte von ihrem Mittelwert.

    \begin{equation*} s_x^2 = {\frac 1 n \sum_{i=1}^n (x_i - \bar x)^2 \end{equation*}

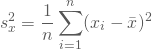
Durch die Quadrierung der Differenzen vermeidest Du zum einen, dass sich positive und negative Abweichungen gegenseitig neutralisieren, und bewirkst zum anderen, dass größere Abweichungen und damit auch Ausreißer stärker berücksichtigt werden. Dadurch wird ihre intuitive Interpretation allerdings schwieriger.

Als Ergebnisse der Statistikklausur wurden beispielsweise ausgehängt:

Student 1 2 3 4 5
Punkte 15 12 14 9 8

Berechnung der Stichprobenvarianz

Die mittlere Punktzahl beträgt \bar x = \frac 1 n \sum_{i=1}^n x_i = 11,6 und Du berechnest die empirische Varianz dementsprechend zu

    \begin{equation*} s_x^2 = \frac 1 5 [(15-11,6)^2+(12-11,6)^2+(14-11,6)^2+(9-11,6)^2 +(8-11,6)^2 ]= = 7,44 \end{equation*}

Im Fall von gruppiertem Datenmaterials kennst Du anstelle des exakten Beobachtungswertes nur seine Gruppenzugehörigkeit. Dann ersetzt Du bei der Berechnung des arithmetischen Mittels \bar x und in der Varianzformel die Beobachtungswerte durch die jeweilige Gruppenmitte. Falls mehr als ein Beobachtungswert in der i-ten Gruppe liegt, wird die Gruppenmitte mit n_i multipliziert.

    \begin{equation*} s_x^2 = \frac 1 n \sum_{i=1}^k n_i \cdot (x_i^m - \bar x)^2, \quad mit \quad \bar x = \frac 1 n \sum_{i=1}^k n_i \cdot x_i^m \quad und \quad n = \sum_{i=1}^k n_i \quad \end{equation*}

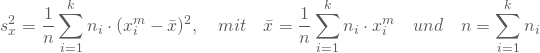
Die Klausur im Fach Marketing haben 50 Studenten mitgeschrieben; ihr Notenspiegel ist in den ersten beiden Spalten der Tabelle gegeben:

Gruppe i Punkte x_i^u bis x_i^o Anzahl n_i Gruppenmitte x_i^m Berechnung des arithmetischen Mittels n_i \cdot x_i^m Berechnung der Varianz n_i \cdot (x_i^m - \bar x)^2
1 13 bis 15 12 14 168 188,179
2 10 bis 12 17 11 187 15,667
3 7
bis 9		 15 8 120 62,424
4 4
bis 6		 5 5 25 127,008
5 1 bis 3 1 2 2 64,642
Summe 50 502 457,920
\frac 1 n \cdot Summe 10,04 9,158

Die durchschnittliche Punktzahl wird als arithmetisches Mittel zu 10,04 Punkten ermittelt; die Varianz der Punktzahlen beträgt folglich 9,158.

Die empirische Varianz gehört übrigens zu den am häufigsten verwendeten Streuungsmaßen und bildet die Grundlage für die Berechnung von Standardabweichung und Standardfehler.