Standardfehler

Standardfehler

  • 7. September 2017
  • Posted by: Mika
Keine Kommentare

Der Standardfehler ist ein Maß für die mittlere Abweichung des aus einer Stichprobe berechneten Mittelwerts von dem tatsächlichen Mittelwert der Grundgesamtheit.

Stell Dir vor, Du möchtest wissen, wie hoch die Mietausgaben der Philosophiestudenten des ersten Semesters in Freiburg sind. Zum einen könntest Du die Mietausgaben x_i für alle n=1000 Erstsemestler erheben und daraus den Mittelwert sowie als Streuungsmaß die Standardabweichung berechnen:

    \begin{equation*} \bar x = \frac 1 n \sum_{ i=1}^n x_i \quad und \quad s_x = \sqrt {\frac 1 n \displaystyle \sum_{i=1}^n (x_i - \bar x)^2 } \end{equation*}

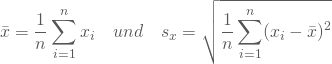
Diese Erhebung wäre vollständig, aber mit hohem Aufwand und Kosten verbunden.

Alternativ könntest Du eine zufällig ausgewählte Stichprobe der Studenten ziehen und aus dieser Stichprobe den Mittelwert \bar x' und s_x^' ermitteln. Diese Werte können Dir mit wesentlich geringerem Erhebungsaufwand brauchbare Maßzahlen liefern, die aber solange mit Fehlern behaftet sind, bis die komplette Grundgesamtheit mit in die Berechnung eingegangen ist. Der Fehler wird umso geringer, je größer Deine Stichprobenerhebung wird.

Was ist nun der Standardfehler?

Der Standardfehler SF ist ein Maß für die Abweichung Deines Stichprobenmittelwertes \bar x^' von dem tatsächlichen Mittelwert \bar x. Er ist definiert als Quotient aus der Standardabweichung Deiner Stichprobe und der Wurzel aus dem Stichprobenumfang:

    \begin{equation*} SF = \frac {s_x} { \sqrt n} = \frac {\sqrt {\frac 1 n \displaystyle \sum_{i=1}^n (x_i - \bar x)^2}} { \sqrt n} \end{equation*}

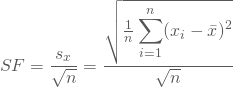
Die Tabelle zeigt Dir, wie sich die mittlere Abweichung des berechneten vom tatsächlichen Mittelwert bei gleicher Standardabweichung aber zunehmendem Stichprobenumfang verringert:

Stichprobenumfang
 n_j Standardabweichung
 s_{xj}^' Standardfehler
 \frac { s_{xj}^'} {\sqrt n}
10 50 15,81
100 50 5,00
500 50 2,24