Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Wölbung (Exzess, Kurtosis)
- 30. Oktober 2017
- Posted by: Mika
Die Wölbung oder Kurtosis einer Häufigkeitsverteilung liefert Dir ein Maß für ihre Spitzheit oder Flachheit.
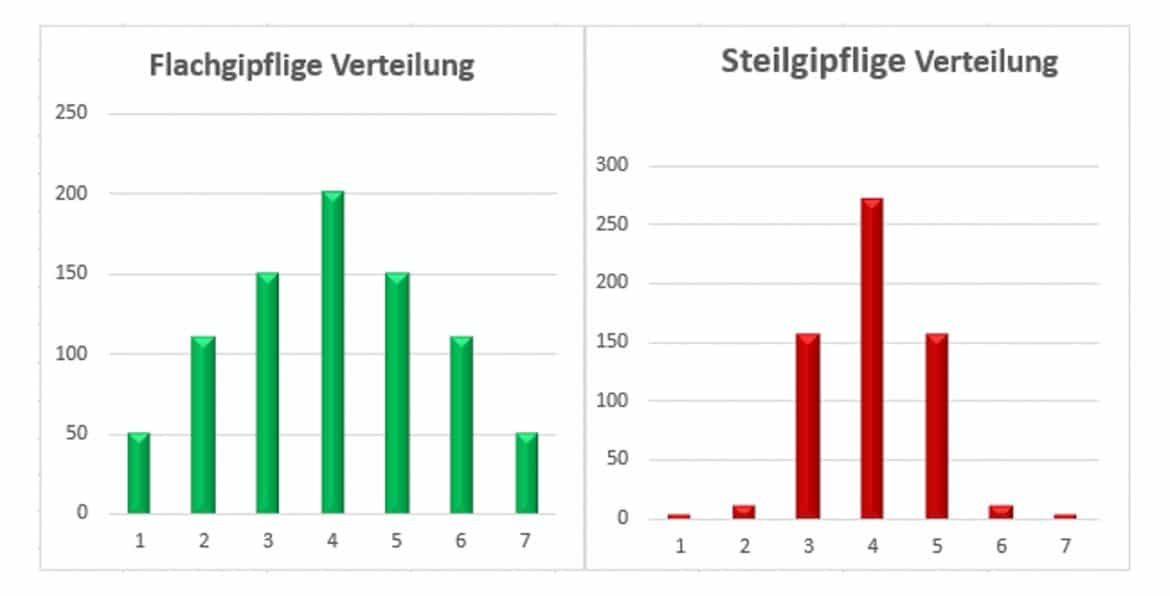
In den Häufigkeitsverteilungen werden 810 bzw. 602 Personen auf 7 Größenklassen aufgeteilt.
Im linken Fall sind alle Größenklassen deutlich mit Personen belegt, entfernt von der Mitte sinken die Häufigkeiten dagegen, wenn auch langsam. In einem solchen Fall spricht man von einer flachgipfligen oder platykurtischen Verteilung mit geringer Kurtosis.
Im rechten Fall ballen sich die Häufigkeiten in den mittleren Größenklassen und flachen nach außen hin sehr stark ab; in einem solchen Fall spricht man von einer steilgipfligen oder leptokurtischen Verteilung mit hoher Wölbung.
Wie berechnet man die Wölbung / Kurtosis?
Als Maß für den Grad der Flach- oder Steilgipfligkeit kannst Du die Wölbung ![]() Deiner empirischen Verteilung als das vierte empirische Moment berechnen:
Deiner empirischen Verteilung als das vierte empirische Moment berechnen:
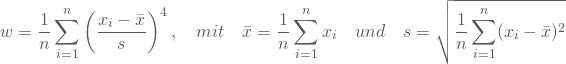
Da die Größe ![]() aus vierten Potenzen besteht, ist ihr Wert immer positiv; je geringer die Wölbung ist, umso flachgipfliger ist Deine Verteilung.
aus vierten Potenzen besteht, ist ihr Wert immer positiv; je geringer die Wölbung ist, umso flachgipfliger ist Deine Verteilung.
Berechnung des Exzesses
Als Grenze zwischen flachgipfliger und steilgipfliger Verteilung wird das Wölbungsmaß der Normalverteilung gesetzt, das übrigens einen Wert von 3 aufweist.
Deshalb wählt man für die Beurteilung einer Verteilung oft anstelle der Wölbung den Exzess, der sich durch Subtrahieren von 3 vom Wert der Wölbung ergibt:
![]()
Anhand des Exzesses einer Verteilung kannst Du die Einteilung dann noch einfacher anhand des Vorzeichens vornehmen, wie Entscheidungsregeln der Tabelle aufzeigen.
In der dritten Tabellenspalte findest Du die Bezeichnung, die in der Literatur häufig auftaucht.
| Wert | Beschreibung | Bezeichnung |
| Excess < 0 | flachgipflige Verteilung | platykurtische Verteilung |
| Excess = 0 | normalgipflige Verteilung | mesokurtische Verteilung |
| Excess > 0 | steilgipflige Verteilung | leptokurtische Verteilung |
