Schiefe

Schiefe

  • 30. Oktober 2017
  • Posted by: Mika
Keine Kommentare

Oft ist eine Verteilung nicht symmetrisch um ihre Mitte herum angeordnet, sondern „fällt“ in eine Richtung. Die Grafik zeigt neben der symmetrischen grauen Verteilung in der Mitte eine linksschiefe (oder rechtssteile) Verteilung in grün und eine rechtsschiefe (oder auch linkssteile) Verteilung in rot auf der rechten Seite.

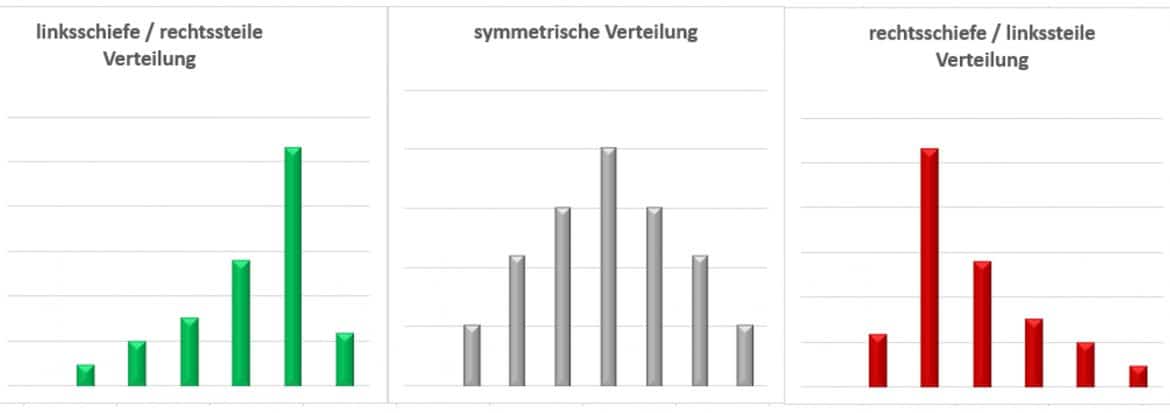
Schiefe

Wie wird die Schiefe berechnet?

Als Maß für Art und Stärke der Asymmetrie kannst Du die Schiefe v Deiner empirischen Verteilung als das dritte empirische Moment berechnen:

    \begin{equation*} v = \frac 1 n \sum_{i=1}^n \left( \frac {x_i - \bar x} s \right) ^3, \quad mit \quad \bar x = \frac 1 n \sum_{i=1}^n x_i \quad und \quad s = \frac {1} {n} \sum_{i=1}^n (x_i-\bar x)^2 \end{equation*}

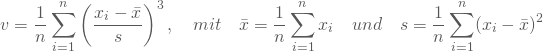
Bei einer symmetrischen Verteilung erhältst Du also für v den Wert Null. Ist v größer als Null, dann liegt eine rechtsschiefe / linkssteile Verteilung vor; im Fall eines negativen Wertes von v ist die Verteilung linksschief bzw. rechtssteil.

Die Altersverteilung der Mitarbeiter eines Unternehmens ist beispielsweise in der Tabelle gegeben:

1 2 3 4 5 6 7 8 9 10 \bar x s
18 23 27 31 34 39 42 45 52 65 37,6 13,4179

Daraus berechnest Du die Schiefe der Verteilung also mit der folgenden Formel:

    \begin{equation*} v = \frac 1 {10} \displaystyle\sum_{i=1}^{10} \left( \frac {x_i - 37,6} {13,41} \right) ^3 = 0,4919 \end{equation*}

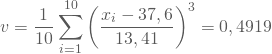
Mit v > 0 liegt demnach eine rechtsschiefe / linkssteile Verteilung wie die der roten Grafik vor: Bei einem durchschnittlichen Alter von 37,6 Jahren handelt es sich um eine Belegschaft mit vielen jungen und einigen wenigen älteren Mitarbeitern.