Median

Median

  • 8. September 2017
  • Posted by: Mika
Keine Kommentare

Um den Median Deiner mindestens ordinalskalierten Beobachtungswerte zu bestimmen, ordnest Du zunächst die Werte der Größe nach an. Ihr Median ist dann derjenige Wert, der die „Grenze“ zwischen den 50% unteren und den 50% oberen Beobachtungen bildet.

Bei seiner Bestimmung unterscheidest Du nach der Anzahl von Beobachtungswerten:

  • im Fall einer ungeraden Anzahl (n=2k+1) ist der Median gleich dem mittleren Wert;
  • bei einer geraden Anzahl von Beobachtungswerten (n=2k) dagegen nimmst Du die beiden mittleren Werte und bildest ihr arithmetische Mittel.

    \begin{equation*} \bar x_{med} =\begin{cases} x_{k+1} \quad f\"ur \quad n=2k+1 \\ \quad \\ \frac 1 2 ( x_{k}+x_{k+1})\quad f\"ur \quad n=2k \end{cases}\end{equation*}

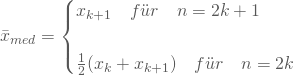
Beispielberechnung für den Median

Messungen der Wuchshöhe von einjährigen Kirschlorbeersträuchern ergaben die folgenden Werte in Zentimetern, die bereits der Größe nach geordnet wurden:

x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9
62,5 cm 63,0 cm 64,2 cm 64,2 cm 65,3 cm 65,7 cm 66,1 cm 66,2 cm 70,0 cm

Da die Anzahl n=9 der Beobachtungswerte ungerade ist, kannst Du als Median direkt den fünften (mittleren) Wert ablesen:

    \begin{equation*} \bar x_{med} = x_5 = 65,3 \end{equation*}

Man betrachtet nur den bzw. die mittleren Werte und die Informationen der übrigen Beobachtungswerte gehen (im Unterschied etwa zum arithmetischen Mittel) nicht in die Berechnung dieses Lageparameters ein. Dadurch ist er unempfindlich gegenüber Ausreißern; und wird daher als robustes Maß bezeichnet.

Er gehört zur Gruppe der Quantile und wird durch das 50\%-Quantil dargestellt.