Harmonisches Mittel

Harmonisches Mittel

  • 8. September 2017
  • Posted by: Mika
Keine Kommentare

Harmonisches Mittel als spezieller Mittelwert: Wenn sich Deine Beobachtungen auf Brüche mit konstantem Nenner zurückführen lassen, kannst Du anstelle des gewichteten arithmetischen Mittels alternativ das harmonische Mittel mit weniger Rechenaufwand bestimmen. Das folgende Beispiel zeigt das:

Stell Dir vor, Du kaufst täglich für 5 Euro Äpfel, wobei der Preis variiert. Du erhältst also für den gleichen Betrag jeden Tag eine unterschiedliche Anzahl von Äpfeln. Dich interessiert, wieviel Du im Mittel pro Stück bezahlst, und dokumentierst dazu Deinen Einkauf an fünf Tagen:

Tag Anzahl Preis pro Apfel
1 8 0,63 €
2 5 1,00 €
3 7 0,71 €
4 6 0,83 €
5 4 1,25 €

Falsch wäre es, das einfache arithmetische Mittel aus den Preisen pro Apfel zu berechnen, da Du ja für den festen Betrag von fünf Euro täglich einkaufst und je nach Tagespreis eine unterschiedliche Stückzahl erhältst. Richtig dagegen wäre es, das mit den Anzahlen gewichtete arithmetische Mittel zu bestimmen:

    \begin{equation*} \bar x_{arith} = \frac {8 \cdot 0,63 + 5 \cdot 1 +7 \cdot 0,71+6 \cdot 0,83 +4 \cdot 1,25} { 8+5+7+6+4}= \frac {25 } {30 } = 0,83 \end{equation*}

Harmonisches Mittel: Rechenbeispiel

Schneller und mit weniger Rechenaufwand erhältst Du das gleiche Ergebnis, indem Du den Quotienten aus der Anzahl der Tage und der summierten Kehrwerte der Apfelpreise bildest:

    \begin{equation*} \bar x_{harm} = \frac {5} {\frac 1 {0,63 }+ \frac 1 {1,00 }+\frac 1 {0,71}+\frac 1 {0,83 }+\frac 1 {1,25}}= \frac {5 } {6 } = 0,83\end{equation*}

Allgemein berechnest Du das harmonische Mittel als Quotienten aus der Anzahl unterschiedlicher Beobachtungswerte und deren summierten Kehrwerten:

    \begin{equation*} \bar x_{harm} = \frac {\quad n \quad} {\displaystyle\sum_{i=1}^n \frac 1 {x_i }} \end{equation*}

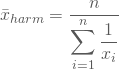
Diese auf den ersten Blick nicht immer intuitive Maßzahl ist etwa auch beim Mitteln von Geschwindigkeiten oder allgemein für Verhältniszahlen nützlich.

Achtung: Geometrischen Mittel und Arithmetisches Mittel sind hiervon abzugrenzen.