Gini-Index, Lorenzkurve

Gini-Index, Lorenzkurve

  • 30. Oktober 2017
  • Posted by: Mika
Keine Kommentare

Wozu benötigt man Gini-Index, Lorenzkurve? Die Lorenzkurve bietet eine grafische Darstellung der relativen Konzentration einer Verteilung, indem Sie die Häufigkeitsverteilung der Merkmalsträger der der Merkmalssumme gegenüberstellt. Liegt keine Konzentration vor, so treffen sich die beiden Verteilungen auf der Hauptdiagonalen.

Für ein Seminar schließen sich beispielsweise Studenten in Arbeitsgruppen von fünf Studenten zusammen, um gemeinsam eine Präsentation zu erstellen. Der zeitliche Aufwand, den die einzelnen in Deiner Gruppe dafür einsetzen, ist sehr unterschiedlich:

Merkmalsträger

Studenten der Gruppe		 Merkmalssumme

eingesetzte Arbeitsstunden
Zeitaufwand absolute Häufigkeit relative Häufigkeit kumulierte relative Häufigkeit absolute Häufigkeit relative Häufigkeit kumulierte relative Häufigkeit
5 Stunden 1 0,2 0,2 5 0,10 0,10
7 Stunden 2 0,4 0,6 14 0,29 0,39
10 Stunden 1 0,2 0,8 10 0,20 0,59
20 Stunden 1 0,2 1 20 0,41 1,00
Summe 5 1 49 1

In der Tabelle sind aus den absoluten Häufigkeiten zunächst die relativen Häufigkeiten berechnet. Diese ergeben kumuliert die empirische Verteilungsfunktion.

Darstellung der Lorenzkurve

Trägst du nun die kumulierten relativen Häufigkeiten der Merkmalsträger auf der vertikalen und die der Merkmalssumme auf der horizontalen Achse ab, so ergibt sich die Lorenzkurve des Arbeitseinsatzes wie in der folgenden Grafik:

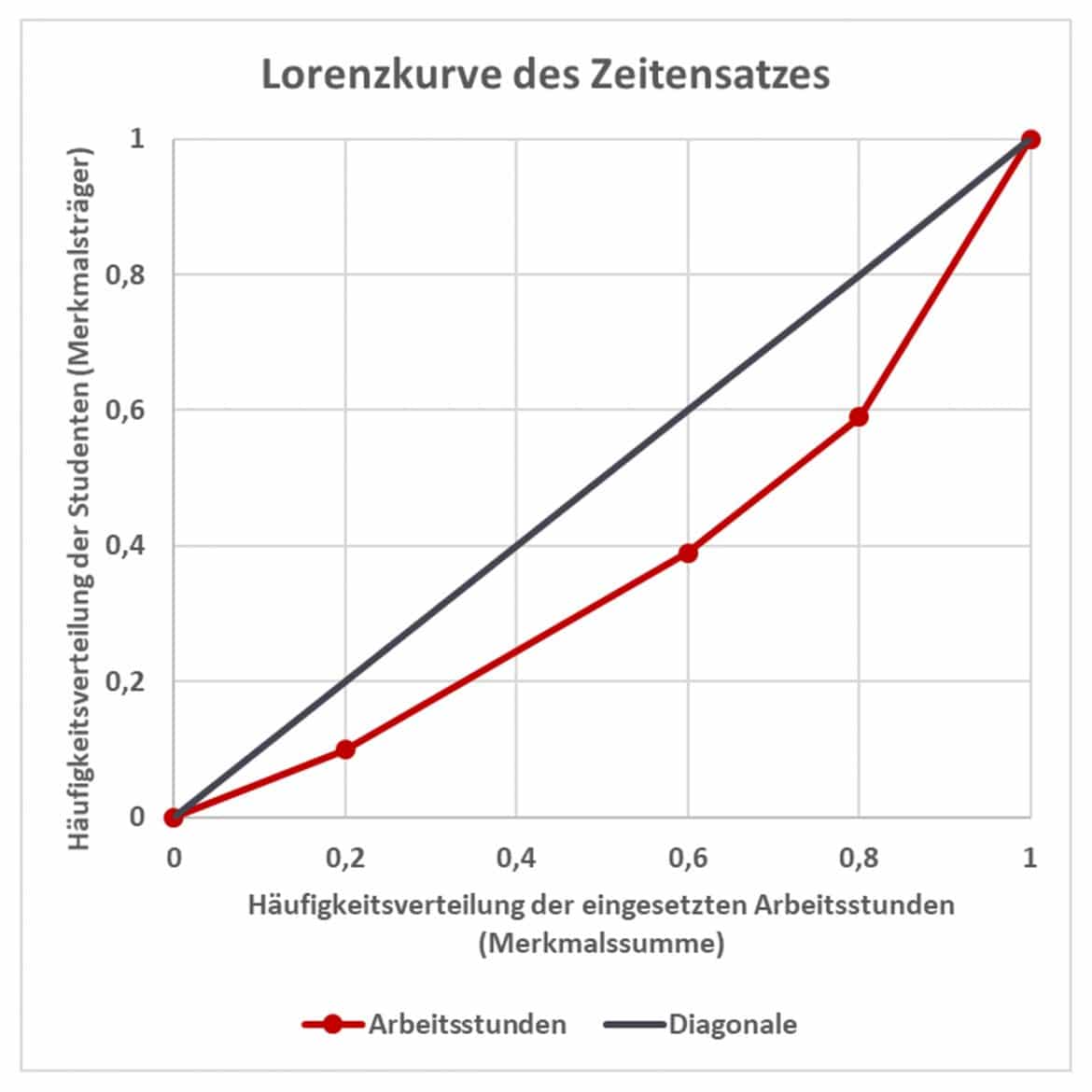
Lorenzkurve

Falls alle Studenten den gleichen Zeiteinsatz aufbrächten, fiele die Lorenzkurve mit der Diagonalen zusammen. In Deinem Beispiel aber wird von den ersten 20 Prozent der Studenten nur 10 Prozent des gesamten Zeiteinsatzes geleistet. Die oberen zwanzig Prozent (das ist der „fleißigste“ Student) dagegen tragen 40 Prozent der eingesetzten Gesamtzeit bei.

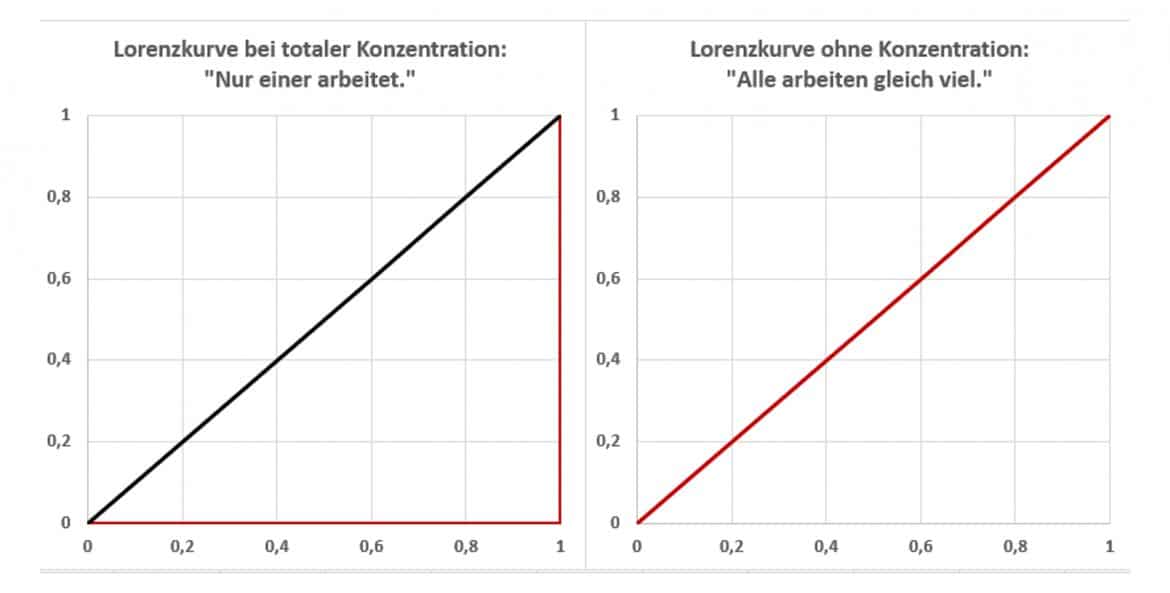
Interpretation der Lorenzkurve

Je weiter die Lorenzkurze von der Diagonalen entfernt ist, umso größer ist die Ungleichverteilung. Im Extremfall, dass die gesamte Merkmalssumme auf einen Merkmalsträger entfällt, fällt die Lorenzkurve mit der x-Achse zusammen.

Lorenzkurven

Berechnung des Gini-Koeffizienten

Der Gini-Koeffizient oder Gini-Index fasst diese grafische Information in einer Zahl zusammen: Er berechnet den Anteil der Fläche zwischen der Diagonalen und der Lorenzkurve an der Fläche unter der Diagonalen:

    \begin{equation*} K = \frac {Fl\"ache \quad zwischen \quad Lorenzkurve\quad und \quad Diagonale } { Fl\"ache \quad des \quad Dreiecks \quad unter \quad der \quad Diagonalen} \end{equation*}

Die Fläche des Inhalts unter der Diagonalen beträgt immer \frac 1 2. Insofern kannst Du den Gini-Index als doppelte Fläche zwischen Lorenzkurve und Diagonale berechnen.

Für Dein Beispiel ermittelst Du als Fläche 1 die Fläche unter der Lorenzkurve, indem Du sie entsprechend der Tabelle in Rechtecke und Dreiecke zerlegst:

    \begin{equation*} \frac { 0,2 \cdot 0,1} { 2} + (0,4 \cdot 0,1) + \frac { 0,4 \cdot 0,29} {2 } + (0,2 \cdot 0,39) + \frac { 0,2 \cdot 0,2} { 2} + (0,59 \cdot 0,2) + \frac { 0,41 \cdot 0,2} {2 } = 0,365 : Fl\"ache 1 \end{equation*}

Der Flächeninhalt zwischen Lorenzkurve und der Diagonalen ergibt sich durch Subtraktion von Fläche1 vom Flächeninhalt unter der Diagonalen zu:

    \begin{equation*} Fl\"ache 2: 0,5 - 0,365 = 0,135 \end{equation*}

und Deinen Gini-Index erhältst Du dann als

    \begin{equation*} K = 2 \cdot Fl\"ache 2 = 0,27 \end{equation*}

Der Zeiteinsatz der verschiedenen Personen weist einen Gini-Index der Konzentration von 0,27 auf.

Problematisch bei der Verwendung des Gini-Indexes als einziges Maß für die Ungleichheit ist, dass verschiedenen Verläufe der Lorenzkurve zum gleichen Flächeninhalt zwischen Lorenzkurve und der Diagonalen führen können. Er ist insofern als alleiniges Maß nicht eindeutig. Zusammen mit der grafischen Darstellung der Lorenzkurve dagegen stellt er aussagekräftige Information zur Verfügung.