Häufigkeitsverteilungen

Häufigkeitsverteilungen

  • 19. Juni 2017
  • Posted by: Mika
Keine Kommentare

Unter der Häufigkeitsverteilung Deiner Erhebung versteht man die tabellarische Aufstellung, wie häufig die Ausprägungen eines oder mehrerer Merkmale beobachtet werden. Dabei kannst Du absolute Häufigkeitsverteilungen, die die Anzahlen von Beobachtungen enthalten, von relativen Häufigkeitsverteilungen unterscheiden, die sich durch die Division der absoluten Häufigkeiten durch die Gesamtzahl der Beobachtungen ergeben und damit die Anteile darstellen. Kumulierte Häufigkeitsverteilungen entstehen bei mindestens ordinalskalierten Merkmalen durch Summieren der relativen Häufigkeiten beginnend mit der kleinsten beobachteten Ausprägung bis zur gerade betrachteten Ausprägung. Sie geben die Anteile der Erhebung an, die höchstens die gerade betrachtete Ausprägung aufweisen.

Absolute und relative Häufigkeiten

Im Rahmen einer unternehmensinternen Erhebung wird unter anderem das Alter der Mitarbeiter erhoben und Du möchtest darstellen, wie sich die Mitarbeiter altersmäßig verteilen. Grundsätzlich könnten alle Altersangaben zwischen 14 bis 90 Jahren auftauchen. Um aussagefähige Informationen zu erhalten, bildest Du Altersklassen mit unteren Werten x_i^u und oberen Werten x_i^o und ermittelst (durch Zählen) zunächst deren absolute Häufigkeiten, hier in der Spalte vier:

Altersklasse von… …bis absolute Häufigkeit relative Häufigkeit kumulierte Häufigkeit
i x_i^u x_i^o n_i h_i F_i
1 14 20 24 0,0399 0,0399
2 21 30 117 0,1944 0,2342
3 31 40 139 0,2309 0,4651
4 41 50 264 0,4385 0,9037
5 51 100 58 0,0963 1
Summe 602 1,000

In der Tabelle steht n_i für die absolute Häufigkeit, h_i für die relative Häufigkeit und F_i für die kumulierte relative Häufigkeit. Die absoluten Häufigkeiten sind von der Gesamtanzahl der Beobachtungen bestimmt und es ist schwierig, zwei verschiedenen Erhebungen miteinander zu vergleichen. Um bessere Vergleichbarkeit zu erhalten, dividierst Du die absoluten Häufigkeiten n_i durch die Gesamtanzahl n und erhältst die relativen Häufigkeiten h_i = \frac {n_{i}} n, die hier in der fünften Spalte gegeben sind.

In der Altersklasse 3 beispielsweise, die Mitarbeiter im Alter von 31 bis 40 Jahren umfasst, hat das Unternehmen 139 Mitarbeiter. Ihr Anteil beträgt 0,2309 oder 23,09 \% der insgesamt 602 Mitarbeiter.

Kumulierte Häufigkeiten

Für die kumulierte Häufigkeit bis zur Altersklasse i addierst Du zum Wert ihrer relativen Häufigkeit die relativen Häufigkeiten aller kleineren Ausprägungen. Sie sind in der Spalte sechs gegeben.

Die Mitarbeiter bis zur Altersklasse 3 werden unternehmensintern als „jüngere Mitarbeiter“ bezeichnet. Deren Anteil ist in der Spalte F_i als 0,4651 ausgewiesen und ergibt sich als Summe der ersten drei relativen Häufigkeiten der Spalte fünf. Kumulierte Häufigkeitsverteilungen lassen sich natürlich nur für mindestens ordinalskalierte Merkmale erstellen.

Mehrdimensionale Häufigkeiten

Hast Du mehr als ein Merkmal zu Deinen Beobachtungsobjekten erhoben, so kannst Du aus deiner Erhebung mehrdimensionale Häufigkeiten berechnen. Für den zweidimensionalen Fall geben diese die Häufigkeiten an, mit denen die Kombination der i-ten Ausprägung des ersten Merkmals mit der j-ten Ausprägung des zweiten Merkmals auftritt.

Für Deine Erhebung der Mitarbeiter des Unternehmens hast Du etwa zusätzlich zum Alter das Merkmal Geschlecht erhoben. Dann könnte sich Deine absolute zweidimensionale Häufigkeitsverteilung mit n_{ij} als der Anzahl von Personen, die der i-ten Altersklasse und dem j-ten Geschlecht zugehören, wie in der folgenden Tabelle dargestellt, ergeben:

absolute zweidimensionale Häufigkeitsverteilung
n_{ij} Altersklasse von… …bis weiblich männlich Summe
i x_iû x_i^o n_i h_i n_{i \cdot}
1 14 20 13 11 24
2 21 30 54 63 117
3 31 40 37 102 139
4 41 50 99 165 264
5 50 100 35 23 58
Summe n_{i\cdot j} 238 364 602

Visualisierung mehrdimensionaler Häufigkeiten

Die Grafik visualisiert Deine Tabelle:

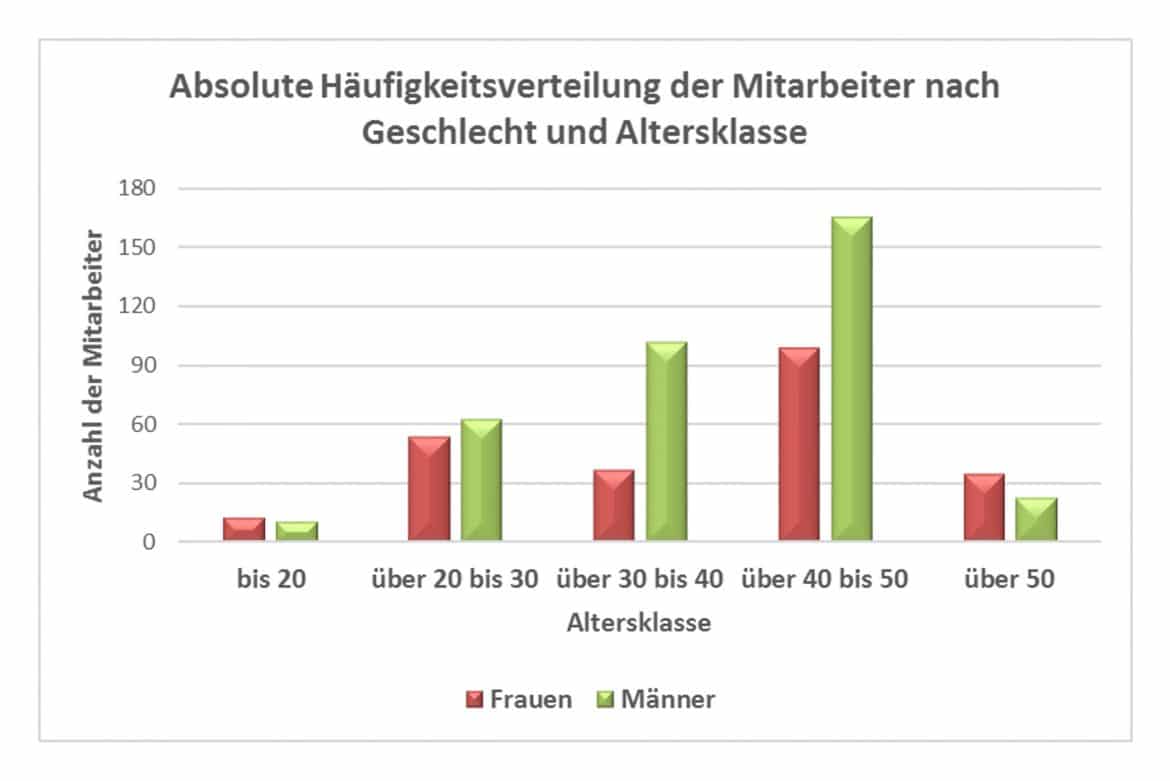
absolute Häufigkeitsverteilung

Interessieren Dich anstelle der absoluten Zahlen die Anteile der Belegschaft, die sich in einer bestimmten Altersklasse befinden und männlich oder weiblich sind, so dividierst Du die absoluten Häufigkeiten n_{ij} durch die Gesamtzahl n der Mitarbeiter und erhältst relative zweidimensionale Häufigkeiten h_{ij}:

relative zweidimensionale Häufigkeitsverteilung
h_{ij}=\frac {n_{ij}} n Altersklasse von… …bis weiblich männlich Summe
i x_iû x_i^o h_i h_i h_{i \cdot}
1 14 20 0,0216 0,0183 0,0399
2 21 30 0,0897 0,1047 0,1944
3 31 40 0,0615 0,1694 0,2309
4 41 50 0,1645 0,2741 0,4385
5 50 100 0,0581 0,0382 0,0963
Summe h_{i\cdot j} 0,3953 0,6047 1,0000

Der Anteil der weiblichen Mitarbeiter in der Altergruppe „41 bis 50 Jahre“ an der Gesamtbelegschaft etwa beträgt 0,1645 oder 16,45 \%.

Die Werte an den Rändern sind die relativen Randhäufigkeiten h_{i \cdot}, die die relative Häufigkeit der i-ten Ausprägung des ersten Merkmals ohne Berücksichtigung des Geschlechts darstellt, sowie die h_{ \cdot j} als relative Häufigkeit, mit der das Geschlecht j ohne Berücksichtigung der Altersklasse beobachtet wurde; die Randhäufigkeiten sind gleich den eindimensionalen Häufigkeiten.

Bedingte Häufigkeitsverteilungen

Interessieren Dich die Anteile verschiedener Merkmalsausprägungen an einer Teilmenge der Grundgesamtheit, so spricht man von bedingten Häufigkeitsverteilungen. So kann hier etwa die Altersverteilung innerhalb der weiblichen bzw. männlichen Mitarbeiter von Interesse sein. Du möchtest etwa wissen, wieviel Prozent aller Frauen sich in der Altersklasse 3 befinden.

Während die absoluten Häufigkeiten gleichbleiben, ändern sich die Anteile, da sie jetzt nicht mehr auf alle Mitarbeiter sondern auf die Gesamtanzahlen der Frauen bzw. Männer bezogen werden:

    \begin{equation*} h_{i|w} = \frac {n_{i1}} {n_{\cdot 1}}\quad und \quad h_{i|m} = \frac {n_{i2}} {n_{\cdot 2}} \end{equation*}

Für Dein Beispiel ergibt sich:

Altersklasse bedingte Altersverteilung der Frauen bedingte Altersverteilung der Männer
i n_{i1} h_{i|w} n_{i2} h_{i|m}
1 13 0,0546 11 0,0302
2 54 0,2269 63 0,1731
3 37 0,1555 102 0,2802
4 99 0,4160 165 0,4533
5 35 0,1471 23 0,0632
Summe n_{\cdot 1} = 238 1,0000 n_{\cdot 2} =364 1,0000

In der Altersgruppe 3 etwa befinden sich 15,55 \% der Frauen; von den Männern sind es 28,02 \%.

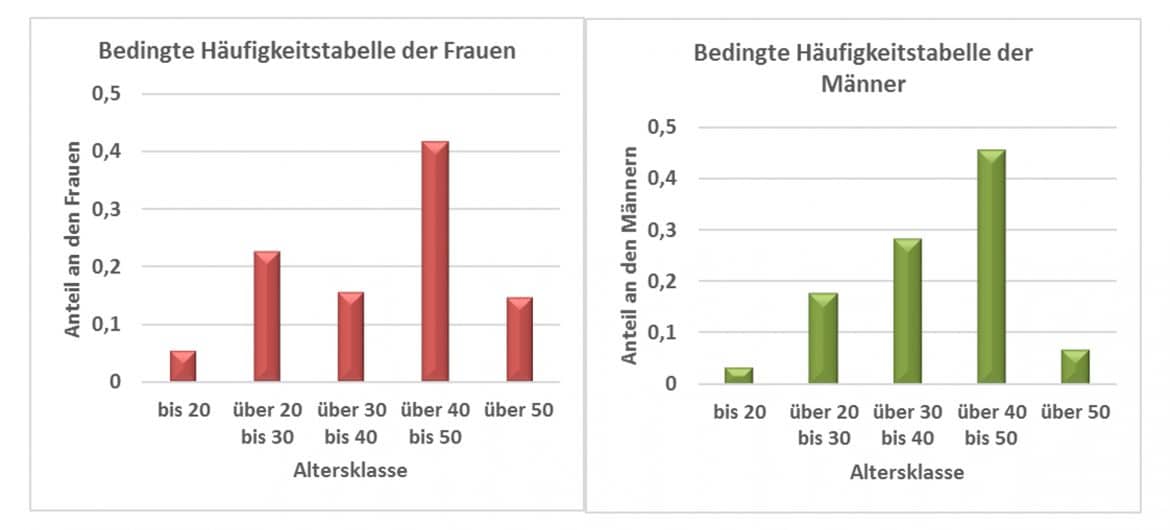
bedingte Häufigkeitsverteilung

Die bedingten Wahrscheinlichkeiten dienen auch dazu, Abhängigkeiten zwischen den Merkmalen aufzuspüren. Falls nämlich das Geschlecht keinen Einfluss auf die Altersverteilung hätte, würden sich die bedingten Altersverteilungen nicht unterscheiden. Das ist hier nicht der Fall.

Für die grafische Darstellung von Häufigkeiten eignen sich bei allen Skalenniveaus besonders Balken- und Säulendiagramme und Boxplots. Im eindimensionalen Fall passen auch Kreisdiagramme. Im Fall von quantitativen Daten ist das Histogramm eine aussagekräftigere Alternative zum Säulendiagramm.