Empirische Verteilungsfunktion

Empirische Verteilungsfunktion

  • 19. Juni 2017
  • Posted by: Mika
Keine Kommentare

Hast Du ein oder mehrere mindestens ordinalskalierte Merkmale erhoben, kannst Du die empirisch Verteilungsfunktion F_i berechnen. Diese ergeben sich direkt aus den relativen Häufigkeiten der Ausprägungen Deiner Erhebung. Sie gibt für die i-te Ausprägung eines Merkmals die Häufigkeiten an, mit der Du diese oder eine kleinere Ausprägung des Merkmals beobachtet hast. Rechnerisch ergibt sie sich folglich als Summe aller relativen Häufigkeiten von Merkmalsausprägungen, die kleiner oder gleich der i-ten Ausprägung sind. Für den eindimensionalen Fall heißt das:

    \begin{equation*} F_i = F(x_i) = \sum_{j=1} ^i h_j = \sum_{j=1} ^i \frac {n_j} n\end{equation*}

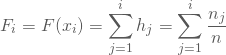
Die Teilnehmer einer Bildungsmaßnahme wurden nach ihrem höchsten Bildungsabschluss befragt und es ergaben sich die folgenden Häufigkeiten:

lfd. Nummer Schulabschluss absolute Häufigkeit relative Häufigkeit empirische Verteilungsfunktion
i n_i h_i=\frac {n_i} n F_i=F(x_i)=\sum_{j=1} ^i h_j
1 Hochschulabschluss  3  0,0811  0,0811
2 Abitur  15  0,4054  0,4865
3 Realschulabschluss  12  0,3243  0,8108
4 Hauptschulabschluss  5  0,1351  0,9459
5 ohne Abschluss  2  0,0541  1,0000
Summe 37 1,0000

Die absoluten und relativen Häufigkeiten lassen sich einfach interpretieren. Von den 37 Befragten gaben beispielsweise 15 Personen an, als höchsten Schulabschluss das Abitur erworben zu haben. Das ist ein Anteil von 0,4054 bzw. 40,54 \%.

Empirische Verteilungsfunktion

Die empirische Verteilungsfunktion kumuliert die relativen Häufigkeiten bis zu der gerade betrachteten Ausprägung. So besagt Ihr Wert in der Zeile der Merkmalsausprägung „3“, dass 81,08 \% der Befragten angaben, mindestens einen Realschulabschluss zu haben.

Betrachtest Du mehr als zwei Merkmale, so kannst Du die empirische Verteilungsfunktion aus den mehrdimensionalen Häufigkeitsverteilungen entsprechend berechnen:

Ein Arzt betreut eine Gruppe von Patienten mit ähnlichem Krankheitsbild und erhebt an ihnen die beiden Merkmale Körpergröße und Gewicht. Er klassifiziert beide Merkmale und erhält die folgende absolute bzw. relative Häufigkeitsverteilung:

Absolute und relative Häufigkeiten einer zweidimensionalen Häufigkeitsverteilung
i Körpergröße
Intervall		 unter 1,55 m 1,55m bis 1,70 m ab 1,71 m Summe
n_{i1} h_{i1} n_{i2} h_{i2} n_{i3} h_{i3} n_{i \cdot} h_{i c\dot}
1 bis 60 kg n_{1j} 10  0,1887 3  0,0566 1  0,0189 14  0,2642
2 61 bis 70 kg n_{2j} 5  0,0943 9  0,1698 6  0,1132 20  0,3774
3 71 bis 80 kg n_{3j} 1  0,0189 4  0,0755 11  0,2075 16  0,3019
4 über 80 kg n_{4j} 0  – 1  0,0189 2  0,0377 3  0,0566
Summe n_{\cdot j} 16  0,3019 17  0,3208 20  0,3774 53  1,0000

Durch Kumulieren der relativen Häufigkeiten gelangst Du zur zweidimensionalen empirischen Verteilungsfunktion:

Empirische Verteilungsfunktion einer zweidimensionalen Häufigkeitsverteilung
i Körpergröße
Gewicht		 unter 1,55 m 1,55m bis 1,70 m ab 1,71 m
F_{i1} F_{i2} F_{i3}
1 bis 60 kg F_{1j} 0,1887 0,2453 0,2642
2 61 bis 70 kg F_{2j} 0,2830 0,5094 0,6415
3 71 bis 80 kg F_{3j} 0,3019 0,6038 0,9434
4 über 80 kg F_{4j} 0,3019 0,6226 1,0000

Die zweidimensionale empirische Verteilungsfunktion besagt etwa, dass ein Anteil von 0,5094 oder 50,94 \% der untersuchten Personen höchstens 1,70 m groß und 70 kg schwer sind. Zudem sind von den Patienten 28,30 \% unter 1,55 m groß und wiegen höchstes 70 kg.