Ausreißer

Unter Ausreißern kannst Du Datenwerte Deiner Stichprobe verstehen, die auffällig höher oder niedriger als Deine übrigen Werte sind und nicht zu den übrigen Werten zu passen scheinen.

Untersuchst Du etwa das Alter der Architekturstudenten zum Zeitpunkt des Bachelor-Abschlusses, könntest Du folgende der Größe nach geordneten Werte erhalten:

19, 20, 20, 20, 21, 21, 22, 22, 22, 22, 23, 23, 23, 24, 24, 25, 25, 72

Der letzte Wert fällt offensichtlich aus der Reihe; hier hat wohl entweder ein Senior das reguläre Studium absolviert oder es liegt ein Schreibfehler vor: Du hast einen Ausreißer vorliegen. Egal woran dieser extreme Wert liegt, beeinflusst er viele statistische Kennzahlen.

So liegt der Mittelwert, d.h. das durchschnittliche Abschlussalter ohne den Ausreißer, bei Jahren, mit Berücksichtigung des älteren Absolventen bei Jahren. Der Medianwert, das ist das mittlere der der Größe nach geordneten Abschlussalter, beträgt in beiden Fällen den Wert 22. Der Median reagiert also im Gegensatz zum Mittelwert robust auf Ausreißer.

Grafische Analyse zum Aufdecken von Ausreißern

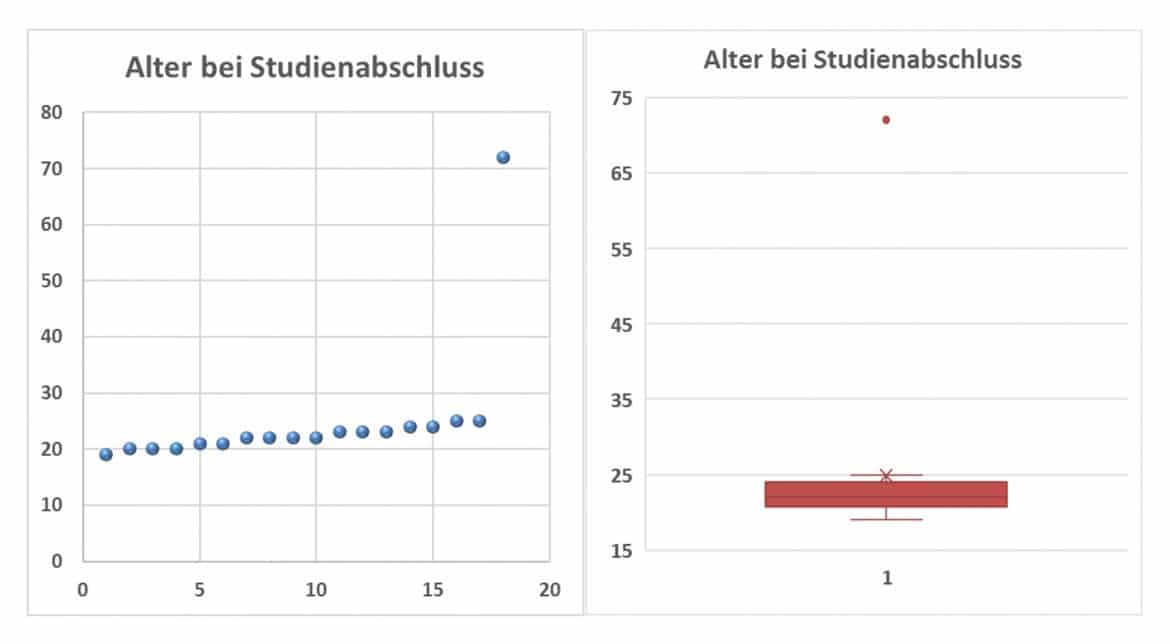
Die erste Grafik zeigt ein einfaches Punktdiagramm: dabei ist deutlich zu erkennen, dass ein Wert ganz aus der Reihe fällt. Die zweite Grafik ist ein Boxplot oder eine Kastengrafik, bei der das hohe Abschlussalter direkt als Ausreißer sichtbar wird.

Behandlung von Ausreißern

Hast Du einen oder mehrere Beobachtungswerte als Ausreißer ausgemacht, so musst Du überlegen, wodurch diese extremen Werte realisiert wurden und dann eine Entscheidung treffen, was mit diesen Werten geschehen soll.

Liegt ein Fehler bei der Datenerhebung oder -eingabe vor, so kannst Du versuchen, ihn zu korrigieren. Ist das nicht möglich, solltest Du die Beobachtung von der weiteren Analyse ausschließen. Letztere Behandlung bietet sich auch an, wenn das Beobachtungsobjekt irrtümlich in die Erhebung aufgenommen wurde.

Angenommen, Du hast die obige Erhebung durchgeführt, um zu untersuchen, in welchem Alter Architekturstudenten auf den Arbeitsmarkt treten. Dann gehört der 72-jährige Absolvent nicht in Deine Analyse hinein und Du solltest ihn von der weiteren Untersuchung ausschließen.

Einige statistische Programmsysteme bieten zudem die Möglichkeit an, pauschal die äußeren Deiner Daten nicht in die Berechnungen mit einzubeziehen. Dabei können aber auch wertvolle Informationen verlorengehen.